Difference between revisions of "Processes & Water Filters (Virtual)"
(1003 --> 1004) |
|||
| (8 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
= Objective = | = Objective = | ||
The | The objective of this lab is to design and assemble a low-cost water filter. A contaminated water supply must first have its acidity neutralized and then the water must be filtered. The filter will be evaluated both on cost and the amount of material it filters out. A process flow diagram will be designed based on the water treatment system guidelines and the physical filter design. | ||
= Overview = | = Overview = | ||
| Line 19: | Line 19: | ||
The first step in the water treatment process is <b>coagulation | The first step in the water treatment process is <b>coagulation and flocculation</b>. This is a process where positively-charged chemicals called flocculants are added to the water to neutralize the negative charge of the contaminants in the water. The contaminants combine with the flocculants to form floc. Floc consists of larger particles that are easier to filter out. In this lab, aluminum sulfate, also known as alum, will be used as the flocculant. | ||
The second step in water treatment is <b>sedimentation</b>. | The second step in water treatment is <b>sedimentation</b>. In this process, floc settles to the bottom of the water supply. | ||
After sedimentation, the water on top of the floc goes through a series of filters that are made up of sandbeds, gravel, or other materials. At some water treatment plants, water also | After sedimentation, the water on top of the floc goes through a series of filters that are made up of sandbeds, gravel, or other materials. At some water treatment plants, water also passes through a granulated carbon filter that removes any organic material and other particles. This step is known as <b>filtration</b>. | ||
After filtration, a disinfectant may be added to kill any remaining bacteria, viruses, or parasites in the process of <b>disinfection</b>. Chlorine is commonly used to treat water and rid it of any chemical pollutants. It is important that all the sediments are removed from the water as chlorine can react with them and produce trihalomethanes, which can cause cancer. Chlorine also produces a residue that will ensure water is disinfected and safe for consumption. | After filtration, a disinfectant may be added to kill any remaining bacteria, viruses, or parasites in the process of <b>disinfection</b>. Chlorine is commonly used to treat water and rid it of any chemical pollutants. It is important that all the sediments are removed from the water as chlorine can react with them and produce trihalomethanes, which can cause cancer. Chlorine also produces a residue that will ensure water is disinfected and safe for consumption. | ||
| Line 40: | Line 40: | ||
The pH of a solution can be measured using a <b>pH strip</b>, which is a piece of filter paper previously soaked in various acid/base indicators. Once placed in a solution, the pH strip will change color based on the acidic or alkaline | The pH of a solution can be measured using a <b>pH strip</b>, which is a piece of filter paper previously soaked in various acid/base indicators. Once placed in a solution, the pH strip will change color based on the acidic or alkaline property of the solution. Based on the color change of the pH strip, the pH of the solution can be approximated (Figure 4). | ||
[[Image:PHstripColor.jpg|500px|thumb|center|Figure 4: Example pH Strip Color Scale]] | [[Image:PHstripColor.jpg|500px|thumb|center|Figure 4: Example pH Strip Color Scale]] | ||
== Process Flow Diagram == | == Process Flow Diagram == | ||
| Line 65: | Line 61: | ||
The <b>law of conservation of mass</b> states that in a closed system, the mass of the system must remain constant over time. A <b>closed system</b> is a type of thermodynamic system where the exchange of energy can take place with the surroundings, but the mass is conserved within the boundaries of the system. An example is a thermos, which may leak heat from the hot beverage it contains, but when properly capped does not allow the liquid to escape. | The <b>law of conservation of mass</b> states that in a closed system, the mass of the system must remain constant over time. A <b>closed system</b> is a type of thermodynamic system where the exchange of energy can take place with the surroundings, but the mass is conserved within the boundaries of the system. An example is a thermos, which may leak heat from the hot beverage it contains, but when properly capped does not allow the liquid to escape. | ||
Applying the law of conservation of mass to a flow chart, the total mass that enters a system must equal the total mass exiting the same system. In Figure 5, the box represents the system, and the arrows into and out of the box represent the movement of mass into and out of the system, respectively. In a continuous process, the mass can be expressed as the mass flow rate. <b>Mass flow rate</b> is the mass of a fluid that passes through a cross-sectional area of the system per unit of time. In Figure 5, 6 | Applying the law of conservation of mass to a flow chart, the total mass that enters a system must equal the total mass exiting the same system. In Figure 5, the box represents the system, and the arrows into and out of the box represent the movement of mass into and out of the system, respectively. In a continuous process, the mass can be expressed as the mass flow rate. <b>Mass flow rate</b> is the mass of a fluid that passes through a cross-sectional area of the system per unit of time. In Figure 5, 6 <math>lb_m</math> of the upper material and 12 <math>lb_m</math> of the lower material enter the system per second that passes. 18 <math>lb_m</math> must leave the system per second to satisfy mass conservation. | ||
[[Image:MassBalanceEx.jpg|600px|thumb|center|Figure 5: Example Mass Balance]] | [[Image:MassBalanceEx.jpg|600px|thumb|center|Figure 5: Example Mass Balance]] | ||
| Line 74: | Line 70: | ||
<p style="text-align:right">(2)</p> | <p style="text-align:right">(2)</p> | ||
In (2), all the materials that are fed into the process unit are | In (2), all the materials that are fed into the process unit are the <b>input</b> and all the product streams that flow out of the process unit are the <b>output</b>. <b>Generation</b> is the amount of materials formed in a process unit and <b>consumption</b> is the amount of materials lost in a process unit. Mass balance is also known as <b>material balance</b>. | ||
== PFD Example == | == PFD Example == | ||
| Line 86: | Line 82: | ||
The complete PFD in Figure 6 is used to describe the general elements of a PFD. | The complete PFD in Figure 6 is used to describe the general elements of a PFD. | ||
<b>Process vessels and equipment</b> are the units that the working stream passes through to have some of its physical properties changed, such as temperature, mass flow, or pressure. Some examples are mixers, steamers, turbines, and reactors. | [[Image:ProcessFlowDiagramEx.jpg|650px|thumb|center|Figure 6: Example Process Flow Diagram]] | ||
<b>Process vessels and equipment</b> are the units that the working stream passes through to have some of its physical properties changed, such as temperature, mass flow, or pressure. Some examples are mixers, steamers, turbines, and reactors. The process vessels are Mixer 1, Mixer 2, Strainer, Trash, and Storage. They can be indicated by different closed form shapes. | |||
The <b>process and utility flow lines</b> include the one-sided arrows in Figure 6, although a process can involve two-sided arrows. The flow lines symbolize the direction in which materials flow and the composition of each stream. | The <b>process and utility flow lines</b> include the one-sided arrows in Figure 6, although a process can involve two-sided arrows. The flow lines symbolize the direction in which materials flow and the composition of each stream. | ||
<b>Full energy and material balance</b> in a process involves | <b>Full energy and material balance</b> in a process involves carrying out the conservation of mass and energy in a process. At Mixer 1, 675 kg/s enters the mixer (500 kg/s of pineapple juice, 100 kg/s of frozen strawberries, and 75 kg/s of fresh peaches), and 675 kg/s leaves the mixer. The mass and energy flow rates are usually listed above the process flow lines. | ||
The <b>composition of the streams</b> is usually listed under the flow lines and indicates the percentage of the streams | The <b>composition of the streams</b> is usually listed under the flow lines and indicates the percentage of the streams of each material. For Mixer 1, the composition of the exit stream is indicated as 74% pineapple juice (P.J.), 15% frozen strawberries (F.S.), and 11% fresh peaches (F.P.). | ||
<b>Bypass and recycle streams</b> are not considered in the PFDs in this lab, but they are also indicated by process flow lines. They consist of streams of undesirable products, such as waste products, that usually flow to a disposable unit. | <b>Bypass and recycle streams</b> are not considered in the PFDs in this lab, but they are also indicated by process flow lines. They consist of streams of undesirable products, such as waste products, that usually flow to a disposable unit. The flow line of 135 kg/s of solid waste that flows into the trash unit is a bypass stream. | ||
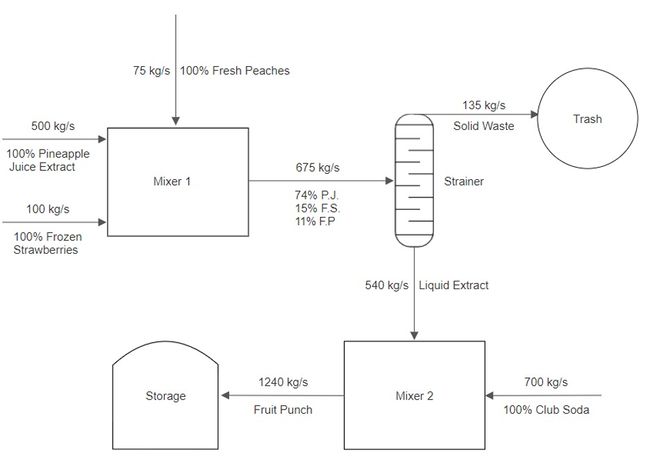
Consider the first part of the example. Three streams enter a mixer and one stream leaves the mixer. There are three inputs and one output, as shown in Figure 7. | |||
[[Image:FirstPartEx.jpg|500px|thumb|center|Figure 7: First Part of Example]] | |||
Keep in mind that each stream should be labeled with the flowrate above the flow line and the composition of the stream below the flow line. Due to mass balance, the flowrate of the product stream is equal to the total flow rate of the input streams. The composition of the product stream can be calculated using (3). | |||
<center><math>Consumption\ of\ Product\ Stream = \frac{Flow\ Rate\ of\ Fruit}{Total\ Flow\ Rate}</math></center> | <center><math>Consumption\ of\ Product\ Stream = \frac{Flow\ Rate\ of\ Fruit}{Total\ Flow\ Rate}</math></center> | ||
| Line 108: | Line 106: | ||
To get the percentage of the concentration, multiply equation (3) by 100. | To get the percentage of the concentration, multiply equation (3) by 100. | ||
Consider the second part of the example. The product stream from Mixer 1 enters a strainer as an input, where 20% of the stream is separated into a solid stream and 80% of the stream is separated into a liquid stream. The solid stream is directed into the trash. The flowrate of the solid and liquid streams can be calculated by multiplying the percentages, 20% and 80%, by the input stream from Mixer 1, as shown in Figure 8. Due to the lack of information, the specific composition of each stream of fruit is unknown in the output and can be omitted in the PFD. | Consider the second part of the example. The product stream from Mixer 1 enters a strainer as an input, where 20% of the stream is separated into a solid stream and 80% of the stream is separated into a liquid stream. The solid stream is directed into the trash. The flowrate of the solid and liquid streams can be calculated by multiplying the percentages, 20% and 80%, by the input stream from Mixer 1, as shown in Figure 8. Due to the lack of information, the specific composition of each stream of fruit is unknown in the output and can be omitted in the PFD. | ||
| Line 121: | Line 116: | ||
[[Image:FinalPartEx.jpg|650px|thumb|center|Figure 9: Final Part of Example]] | [[Image:FinalPartEx.jpg|650px|thumb|center|Figure 9: Final Part of Example]] | ||
= Design Consideration = | = Filter Design Consideration = | ||
* Which aspects of the competition ratio are most advantageous (see 2. Water Filter Design and Assembly below)? | * Which aspects of the competition ratio are most advantageous (see 2. Water Filter Design and Assembly below)? | ||
* Which materials will filter large sediments out of the contaminated water? | * Which materials will filter large sediments out of the contaminated water? | ||
* Which materials will purify the water? | * Which materials will purify the water? | ||
* What order of materials would provide the most efficient results? | * What order of materials would provide the most cost efficient results? | ||
= Materials and Equipment = | = Materials and Equipment = | ||
| Line 144: | Line 139: | ||
== Price List == | == Price List == | ||
<center> | |||
{| class="wikitable" | {| class="wikitable" | ||
|+ Table 1: Materials and Costs | |+ Table 1: Materials and Costs | ||
| Line 155: | Line 151: | ||
|- | |- | ||
|} | |} | ||
</center> | |||
= Procedure = | = Procedure = | ||
The simulation for this lab is done virtually and consists of two parts: pH Neutralization & and Water Filter Assembly. | |||
The simulation for this lab is done virtually | |||
== 1. pH Neutralization == | == 1. pH Neutralization == | ||
| Line 171: | Line 162: | ||
# Compare the color on the end of the strip to the pH color chart in Figure 4. | # Compare the color on the end of the strip to the pH color chart in Figure 4. | ||
# Record the pH and determine if the contaminated water is acidic or alkaline. | # Record the pH and determine if the contaminated water is acidic or alkaline. | ||
# For acidic water, one method of increasing the pH is to add sodium bicarbonate, | # For acidic water, one method of increasing the pH is to add sodium bicarbonate, commonly known as baking soda, which has a pH of approximately 9. If the solution is acidic, add sodium bicarbonate. The general rule of thumb is to add 1 tsp of baking soda per liter of water. Calculate the number of teaspoons of baking soda needed to neutralize the contaminated water. | ||
# Add the baking soda into the contaminated water and mix well. | # Add the baking soda into the contaminated water and mix well. | ||
# Test the pH of the contaminated water again with the pH strips. | # Test the pH of the contaminated water again with the pH strips. | ||
# Compare the color on the end of the strip to the pH color chart and record the final pH. | # Compare the color on the end of the strip to the pH color chart and record the final pH. | ||
== 2. Water Filter Design and Assembly == | == 2. Water Filter Design Analysis: Warm-Up Exercise == | ||
In this exercise, the relationship between % mass lost and the quantity of each material will be analyzed, given that the quantity of one material is varied at a time for the filter keeping the quantity of other two materials constant. The models are merely approximations and they are not accurate representations of the filter process. | |||
#Download the [[Media:Lab_Data_Sheet_Filter.xlsx| Lab 8 Data Sheet]] containing data for this exercise. | |||
#The following steps outline the procedure to create a scatter plot for the sand-varied filter dataset. | |||
##On the Excel ribbon, click on the Insert tab. Navigate to the Insert Scatter option in the Charts groups and click Scatter. This will create a blank scatter plot as shown in Figure 10. | |||
##;[[Image:Lab_ScatterPlot_Filter.jpg|500px|thumb|center|Figure 10: Inserting a Scatter Plot]] | |||
##Right-click on the empty graph and click Select Data. The Select Data Source dialog box will appear. | |||
##Click Add to add a new dataset to the graph. Enter the series name” % Mass Lost vs Scoops of Sand. | |||
##For Series X values, highlight the cells containing the number of teaspoons of sand from the sand-varied filter dataset (A9:A12). For Series Y values, highlight the % mass lost data for the sand-varied filter (D9:D12). | |||
##Rename the axis and chart titles by clicking the Chart Design tab on the Excel Ribbon, then navigating to Add Chart Element and selecting the appropriate Title option. | |||
##To insert a trendline, select Add Chart Element, then navigate to the Trendline option and select Linear. | |||
##Double click on the newly created trendline. A Format Trendline dialog box will appear on the right side of the Excel window. | |||
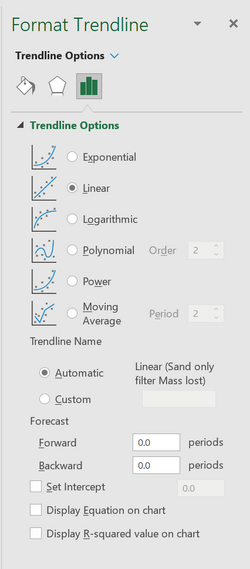
##Click on the Trendline options category with the icon that looks like a column chart, as shown in Figure 11. Check off Display Equation on the chart. | |||
##;[[Image:Lab_Trendline_Filter.jpg|250px|thumb|center|Figure 11: Format Trendline Dialog Box]] | |||
##The finished scatter plot should look like Figure 12. | |||
##;[[Image:Lab_ScatterPlot_Final_Filter.jpg|500px|thumb|center|Figure 12: Scatter Plot for the Sand-varied Filter]] | |||
#Repeat the above steps to create a scatter plot for the gravel-varied and activated carbon-varied filters. | |||
Pay attention to the linear relationship illustrated by the trendline equation in all three scatter plots. It can be deduced that a filter in which the quantity of all three materials is varied would be represented by a linear model of the form (4). | |||
<center><math>aX + bY+ cZ = d</math></center> | |||
<p style="text-align:right">(4)</p> | |||
In (4), <i>d</i> is the total percent mass lost, <i>a</i> is the teaspoons of sand, <i>b</i> is the teaspoons of gravel, <i>c</i> is the teaspoons of activated carbon, and the constants <i>X, Y, Z</i> correspond to the slope of the trendline for the sand-varied, gravel-varied, and activated-carbon varied filters, respectively. | |||
When data is not provided, as in the tables in this exercise, one can use experimental data to derive the relationship given by (4). The extra credit section at the end of this lab manual focuses on using data from Part 3: Water Filter Design and Assembly to derive and analyze this modeling relationship. | |||
== 3. Water Filter Design and Assembly == | |||
# Access the virtual simulation [https://scratch.mit.edu/projects/399704244 here]. | # Access the virtual simulation [https://scratch.mit.edu/projects/399704244 here]. | ||
# Record the data in the Excel datasheet | # Record the data in the Excel datasheet downloaded in Part 2 of this experiment. | ||
# Weigh the empty beaker and record the mass. Maximize the screen if the reading on the scale is not legible. | # Weigh the empty beaker and record the mass. Maximize the screen if the reading on the scale is not legible. | ||
# Pour 250 mL of the contaminated water into the beaker. Weigh the beaker again and record the mass. | # Pour 250 mL of the contaminated water into the beaker. Weigh the beaker again and record the mass. | ||
| Line 186: | Line 204: | ||
# Weigh the beaker again and calculate the mass of just the solution and the alum. | # Weigh the beaker again and calculate the mass of just the solution and the alum. | ||
# Calculate the mass of the alum in the Excel datasheet. | # Calculate the mass of the alum in the Excel datasheet. | ||
# Based on the available materials in Table 1 and their | # Based on the available materials in Table 1 and their cost, construct a water filter that will most effectively filter the physical sediments. | ||
# Record the following information in the Excel datasheet: | # Record the following information in the Excel datasheet: | ||
## | ## Number of teaspoons of each filter material | ||
## Total cost | ## Total cost | ||
# Weigh the beaker and calculate the mass of just the filtered water. | # Weigh the beaker and calculate the mass of just the filtered water. | ||
# Calculate the percent mass lost using ( | # Calculate the percent mass lost using (5) and record it in the datasheet. The percent mass lost normalizes the mass of the physical sediments that is lost from the contaminated water during filtration.<center><math>%\ Mass\ Lost = \frac{Mass\ of\ Contaminated\ Water - Mass\ of\ Filtered\ Water}{Mass\ of\ Contaminated\ Water} \times 100</math></center><p style="text-align:right">(5)</p> | ||
# Calculate the competition ratio of the filter design using ( | # Calculate the competition ratio of the filter design using (6). The competition ratio judges the preformance the filter is at removing physical sediments from the contaminated water.<center><math>Competition\ Ratio = \frac{%\ Mass\ Lost}{Total\ Cost\left[{$}\right]}</math></center><p style="text-align:right">(6)</p> | ||
# Repeat | # Repeat steps 9-13 two more times with two different water filter designs. Record the data for each design in the Excel datasheet. | ||
== | == 4. Process Flow Diagram == | ||
# Design a simplified industrial water treatment system PFD based on the experiments done in this lab. | # Design a simplified industrial water treatment system PFD based on the experiments done in this lab. EG1004 recommends [https://www.diagrams.net/ Diagrams.net] for creating the PFD. Include: | ||
## pH Neutralization | ## pH Neutralization | ||
## Coagulation and flocculation | ## Coagulation and flocculation | ||
| Line 215: | Line 232: | ||
## Calculate the mass flow rate of filtered water leaving the system. | ## Calculate the mass flow rate of filtered water leaving the system. | ||
<b>Keep in mind the order of filtration and any other process units needed to logically complete the process flow (for example a mixer after adding the alum). See the PFD example in the Overview section for reference. Be mindful of the mass balance ( | <b>Keep in mind the order of filtration and any other process units needed to logically complete the process flow (for example a mixer after adding the alum). See the PFD example in the Overview section for reference. Be mindful of the mass balance (7).</b> | ||
<center><math>Input + Generation = Output + Consumption</math></center><p style="text-align:right">(7)</p> | |||
The lab work is now complete. Refer to the Assignment section for the instructions to prepare the lab report. | |||
== 5. Advanced Modeling (Extra Credit) == | |||
This part of the experiment uses a virtual simulation to create three water filters made from sand, gravel, and charcoal. To model the effect of each filter material on the percent mass lost (4), which as defined in Part 2 relates the number of teaspoons of each material to the percent mass lost, can be formed. Assume that the relationship is linear and takes the form of (8). | |||
<center><math>aX + bY +cZ = d</math></center><p style="text-align:right">(8)</p> | |||
In (8), <i>d</i> is the percent mass lost, <i>a</i> is the teaspoons of sand, <i>b</i> is the teaspoons of gravel, <i>c</i> is the teaspoons of activated carbon, and <i>X, Y, Z</i> are the corresponding constants being solved for. Use Microsoft Excel to solve this matrix based on the data found in the second procedure. | |||
A <b>matrix</b> is an array of numbers, used to summarize data concisely, making it easier to analyze. Take, for example, the system of equations in (9), (10), and (11). | |||
<center><math>X + 2Y - Z = 1</math></center><p style="text-align:right">(9)</p> | |||
<center><math>2X + Y = -2</math></center><p style="text-align:right">(10)</p> | |||
<center><math>X + Y + Z = 1</math></center><p style="text-align:right">(11)</p> | |||
This equation can be solved manually by solving for one variable in terms of the others and doing a few substitutions. This process can be simplified by rewriting the system using matrices. The matrix in (12) represents the system of equations except the terms have been reordered so that the coefficients of the variables can be extracted. | |||
<center>[[Image:Lab_SOE_Matrix_Filter.jpg|200px]]</center><p style="text-align:right">(12)</p> | |||
Thinking of the matrix equation as a regular equation, it would make sense to divide the matrix on the product side by the coefficient matrix, but this is not possible in matrix algebra. The equivalent would be finding the inverse of the coefficient matrix and multiplying that by the product matrix. When a matrix is multiplied by its inverse, the result is the identity matrix that is the matrix equivalent of the value 1 in algebra. When multiplying the product side by the inverse of the coefficient matrix that is dividing one by the other. | |||
It is possible to solve the inverse matrix by hand, but this process can be tedious and time-consuming, especially when there are more than two variables to solve. This part of the experiment will require Excel to solve the system of equations. | |||
In (12), the inverse matrix of the coefficient matrix is calculated to be the matrix in (13) where 1/4 was factored out to make the matrix easier to work with. | |||
<center>[[Image:Lab_Inverse_Matrix_Filter.jpg|200px]]</center><p style="text-align:right">(13)</p> | |||
When the inverse matrix is multiplied by the product matrix, the result is the matrix in (14), where the first value represents x, the second represents y, and the third represents z. | |||
<center>[[Image:Lab_Result_Matrix_Filter.jpg|200px]]</center><p style="text-align:right">(14)</p> | |||
Using these principles, derive an equation for the value <i>d</i> in terms of the values <i>a, b, and c</i>, using the three equations from the start of this example. Assume the relationship between <i>a, b, c, and d</i> is linear (15). | |||
<center><math>aX + bY +cZ = d</math></center><p style="text-align:right">(15)</p> | |||
In (15), x, y, and z are the coefficient values sought. Thinking about the values of the coefficient matrix as known values of a, b, and c, and the values of the product side as the resultant values of d, use the solution just found to derive the expression (16). | |||
<center><math>-2X + 2Y +Z = d</math></center><p style="text-align:right">(16)</p> | |||
For this part of the lab, an expression for the %mass lost in terms of the amount of each material (gravel, sand, and activated carbon) will be derived using the data collected in Part 3: Water Filter Design and Assembly. This can be done by hand, but it is more convenient to use matrix properties and Excel to solve the system of equations. | |||
< | #Using the data collected in Part 2, create three equations, one for every trial, which should be modeled like (15). This will make up the system of equations. | ||
##Let <i>a, b, & c</i> represent the teaspoons of sand, gravel & activated carbon, respectively. | |||
##Let <i>d</i> represent the %Mass Lost for each trial. | |||
###For example, if 1 tsp of sand, 2 tsp of gravel, & 1 tsp of activated carbon were used and there was a 4.5% Mass Lost, the equation would look like <math>X + 2Y +Z = 4.5</math>. | |||
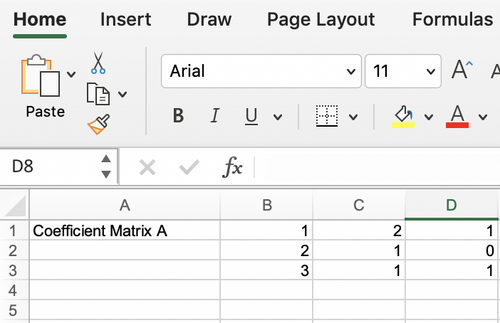
#Create a coefficient matrix (Matrix A) such that (Figure 13) | |||
##coefficients of x are in the first column | |||
##coefficients of y are in the second column | |||
##coefficients of z are in the third column | |||
##;[[Image:Lab_Coefficient_Matrix_Filter.jpg|500px|thumb|center|Figure 13:Coefficient Matrix]] | |||
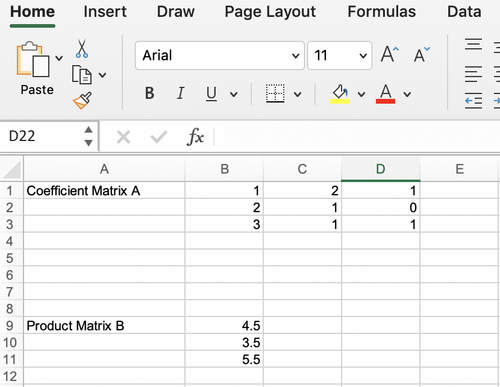
#Create a product matrix (Matrix B) that consists of the %Mass Lost values for each trial (Figure 14). | |||
#;[[Image:Lab_Product_Matrix_Filter.jpg|500px|thumb|center|Figure 14:Product Matrix]] | |||
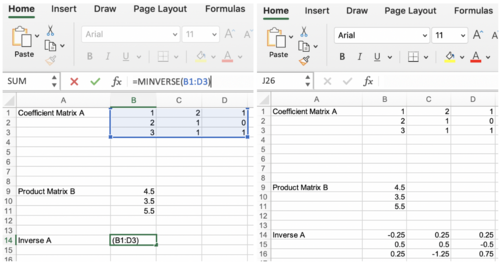
#Find the inverse of Matrix A using Excel’s MINVERSE(array) function, where the array is made up of the values of Matrix A (Cells B1:D3). Note: Before calling the MINVERSE(array) function, highlight the empty cells for the result (Figure 15). | |||
#;[[Image:Lab_Matrix_Results_Filter.jpg|500px|thumb|center|Figure 15:Results]] | |||
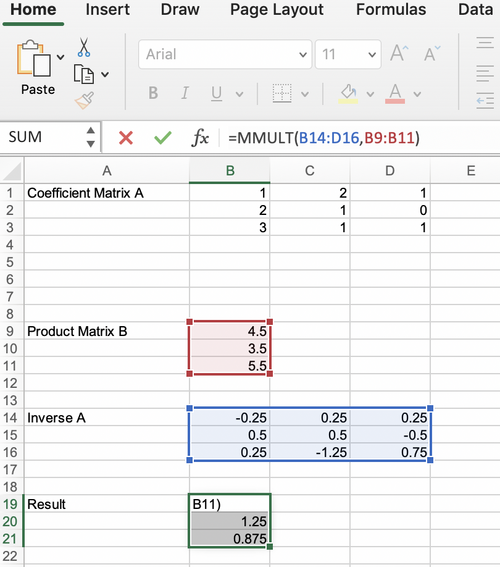
#Solve the system of equations by using Excel’s MMULT(array1, array2) function (Figure 16) | |||
##Array 1 corresponds to the inverse matrix calculated in Step 4. | |||
##Array 2 corresponds to Matrix B created in Step 3. | |||
##;[[Image:Lab_Matrix_Solutions_Filter.jpg|500px|thumb|center|Figure 16:Solutions]] | |||
#The resulting 3x1 matrix represents the values of X, Y, Z | |||
The lab work is now complete. Refer to the Assignment section for the instructions to prepare the lab report. | The lab work is now complete. Refer to the Assignment section for the instructions to prepare the lab report. | ||
| Line 229: | Line 306: | ||
* Describe the water treatment process | * Describe the water treatment process | ||
* What is pH? Why is it important to maintain the pH of drinking water? | * What is pH? Why is it important to maintain the pH of drinking water? | ||
* What was the final pH of the contaminated | * What was the final pH of the contaminated water? | ||
* | * What did alum do to the contaminated water? Discuss any observations | ||
* Discuss minimal design. Describe the importance of minimal design and explain how it was employed in the design. Did the design minimize cost? | * Discuss minimal design. Describe the importance of minimal design and explain how it was employed in the design. Did the design minimize cost? | ||
* Explain the three designs for the water filter, including why certain materials were selected and the order in which they were added | * Explain the three designs for the water filter, including why certain materials were selected and the order in which they were added | ||
* Compare the three designs. Which was the most cost-effective? Which was the cheapest? Which filtered out the most material? | * Compare the three designs. Which was the most cost-effective? Which was the cheapest? Which filtered out the most material? | ||
* | * Which filter media was the most effective at filtering the contaminated water? | ||
* Explain the thought process behind the PFD designed in Part 3 of the procedure. | * Explain the thought process behind the PFD designed in Part 3 of the procedure. | ||
* How might the water filter design be improved (both individual and large scale)? | * How might the water filter design be improved (both individual and large scale)? | ||
* Include pictures of the water filter, the polluted water, the filtered water, the pH strips, and the complete PFD. | * Include pictures of the water filter, the polluted water, the filtered water, the pH strips, and the complete PFD. | ||
* Discuss what part of the lab each member completed for the group and how it was important to the experiment. | |||
{{Labs:Lab Notes}} | {{Labs:Lab Notes}} | ||
Latest revision as of 18:18, 22 August 2022
Objective
The objective of this lab is to design and assemble a low-cost water filter. A contaminated water supply must first have its acidity neutralized and then the water must be filtered. The filter will be evaluated both on cost and the amount of material it filters out. A process flow diagram will be designed based on the water treatment system guidelines and the physical filter design.
Overview
Access to safe drinking water is a privilege that is often taken for granted. One of the United Nation’s 17 goals to sustainably transform the world includes available and sustainable management of water and sanitation for all. According to the United Nations, water scarcity affects more than 40% of the global population. It is also estimated that by 2050, 2.3 billion people are expected to live in areas that experience severe water stress.
To prepare for this extensive scarcity of water, engineers have experimented with different ways of making drinking water more accessible. Currently, water is sourced from freshwater sources such as surface water, which includes lakes, rivers, streams, and oceans. Non-conventional water sources, such as desalinated water, treated wastewater, and agricultural drainage water, are also used. Regardless of how it is sourced, all water must go through a treatment process.
Water Treatment Methods
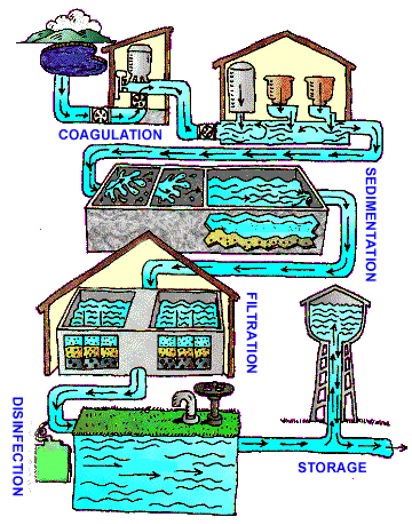
Water is sourced from a reservoir and undergoes treatment to remove contaminants (Figure 2). There are five steps in the water treatment process, however, this lab only covers the first three steps. Note that the water is not safe to drink until the fourth step, disinfection has occurred.
The first step in the water treatment process is coagulation and flocculation. This is a process where positively-charged chemicals called flocculants are added to the water to neutralize the negative charge of the contaminants in the water. The contaminants combine with the flocculants to form floc. Floc consists of larger particles that are easier to filter out. In this lab, aluminum sulfate, also known as alum, will be used as the flocculant.
The second step in water treatment is sedimentation. In this process, floc settles to the bottom of the water supply.
After sedimentation, the water on top of the floc goes through a series of filters that are made up of sandbeds, gravel, or other materials. At some water treatment plants, water also passes through a granulated carbon filter that removes any organic material and other particles. This step is known as filtration.
After filtration, a disinfectant may be added to kill any remaining bacteria, viruses, or parasites in the process of disinfection. Chlorine is commonly used to treat water and rid it of any chemical pollutants. It is important that all the sediments are removed from the water as chlorine can react with them and produce trihalomethanes, which can cause cancer. Chlorine also produces a residue that will ensure water is disinfected and safe for consumption.
Finally, the filtered water is then stored in tanks for future usage.
Water Acidity & Alkalinity
Water and water-based solutions are measured for acidity or alkalinity by their power of hydrogen, or potential for hydrogen (pH). pH is measured on a scale from 0 to 14, and the pH scale is logarithmic based on the concentration of hydrogen ions (1).
(1)
The pH of a solution indicates the concentration of hydrogen ions (H+) and hydroxide ions (OH-). If the concentration of hydrogen ions increases in a solution, it becomes more acidic. If the concentration of hydroxide ions increases, the solution becomes more basic or alkaline. A pH of 0 to 6 indicates an acidic solution and a pH of 8 to 14 indicates an alkaline solution. A pH of 7 indicates a neutral solution, which signifies that the concentration of H+ and OH- ions is equal. The pH scale and examples of solutions of varying pH values can be seen in Figure 3.
The pH of a solution can be measured using a pH strip, which is a piece of filter paper previously soaked in various acid/base indicators. Once placed in a solution, the pH strip will change color based on the acidic or alkaline property of the solution. Based on the color change of the pH strip, the pH of the solution can be approximated (Figure 4).
Process Flow Diagram
In many engineering fields, such as chemical engineering, process flow diagrams (PFD) are used to indicate the sequential movement and processing of a material through multiple processing units and equipment. Drawing PFDs is an essential technique to properly and clearly relay key information about a process design. When drawing PFDs, several elements must be included in the diagram. These elements include:
- Process vessels and equipment
- Process and utility flow lines
- Full energy and material balance
- Composition of every stream
- Bypass and recycle streams
All processes in a PFD must abide by the law of conservation of mass and the law of conservation of energy. Energy conservation is beyond the scope of this introductory lab and will not be considered in the PFDs. Before discussing the elements of a PFD, mass conservation must be introduced.
Mass Balance
The law of conservation of mass states that in a closed system, the mass of the system must remain constant over time. A closed system is a type of thermodynamic system where the exchange of energy can take place with the surroundings, but the mass is conserved within the boundaries of the system. An example is a thermos, which may leak heat from the hot beverage it contains, but when properly capped does not allow the liquid to escape.
Applying the law of conservation of mass to a flow chart, the total mass that enters a system must equal the total mass exiting the same system. In Figure 5, the box represents the system, and the arrows into and out of the box represent the movement of mass into and out of the system, respectively. In a continuous process, the mass can be expressed as the mass flow rate. Mass flow rate is the mass of a fluid that passes through a cross-sectional area of the system per unit of time. In Figure 5, 6 of the upper material and 12 of the lower material enter the system per second that passes. 18 must leave the system per second to satisfy mass conservation.
Mass balance can also be described with a simplified equation (2).
(2)
In (2), all the materials that are fed into the process unit are the input and all the product streams that flow out of the process unit are the output. Generation is the amount of materials formed in a process unit and consumption is the amount of materials lost in a process unit. Mass balance is also known as material balance.
PFD Example
Problem Statement
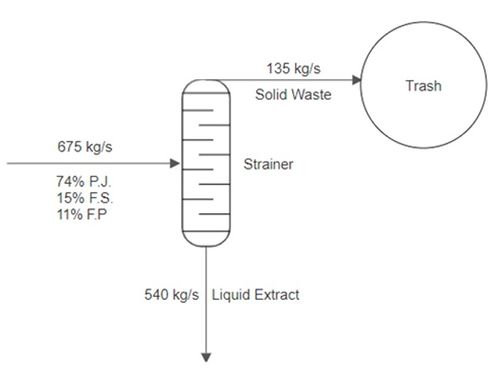
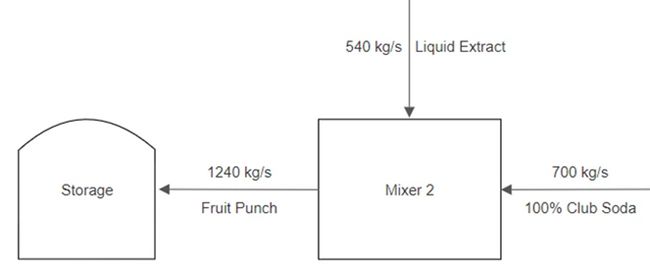
A stream of pineapple juice extract enters a mixer at a rate of 500 kg/s. A stream of frozen strawberries enters the same mixer at a rate of 100 kg/s. A stream of fresh peaches also enters the same mixer at a rate of 75 kg/s. The product stream leaves the first mixer and enters a strainer, where 80% of the mass per second exits in one stream as a liquid. Then 20% of the mass per second exits as a solid and is thrown into the trash. The liquid stream enters a final mixer alongside a stream of club soda that enters at a rate of 700 kg/s. The resulting product stream then enters a storage unit.
PFD Elements
The complete PFD in Figure 6 is used to describe the general elements of a PFD.
Process vessels and equipment are the units that the working stream passes through to have some of its physical properties changed, such as temperature, mass flow, or pressure. Some examples are mixers, steamers, turbines, and reactors. The process vessels are Mixer 1, Mixer 2, Strainer, Trash, and Storage. They can be indicated by different closed form shapes.
The process and utility flow lines include the one-sided arrows in Figure 6, although a process can involve two-sided arrows. The flow lines symbolize the direction in which materials flow and the composition of each stream.
Full energy and material balance in a process involves carrying out the conservation of mass and energy in a process. At Mixer 1, 675 kg/s enters the mixer (500 kg/s of pineapple juice, 100 kg/s of frozen strawberries, and 75 kg/s of fresh peaches), and 675 kg/s leaves the mixer. The mass and energy flow rates are usually listed above the process flow lines.
The composition of the streams is usually listed under the flow lines and indicates the percentage of the streams of each material. For Mixer 1, the composition of the exit stream is indicated as 74% pineapple juice (P.J.), 15% frozen strawberries (F.S.), and 11% fresh peaches (F.P.).
Bypass and recycle streams are not considered in the PFDs in this lab, but they are also indicated by process flow lines. They consist of streams of undesirable products, such as waste products, that usually flow to a disposable unit. The flow line of 135 kg/s of solid waste that flows into the trash unit is a bypass stream.
Consider the first part of the example. Three streams enter a mixer and one stream leaves the mixer. There are three inputs and one output, as shown in Figure 7.
Keep in mind that each stream should be labeled with the flowrate above the flow line and the composition of the stream below the flow line. Due to mass balance, the flowrate of the product stream is equal to the total flow rate of the input streams. The composition of the product stream can be calculated using (3).
(3)
To get the percentage of the concentration, multiply equation (3) by 100.
Consider the second part of the example. The product stream from Mixer 1 enters a strainer as an input, where 20% of the stream is separated into a solid stream and 80% of the stream is separated into a liquid stream. The solid stream is directed into the trash. The flowrate of the solid and liquid streams can be calculated by multiplying the percentages, 20% and 80%, by the input stream from Mixer 1, as shown in Figure 8. Due to the lack of information, the specific composition of each stream of fruit is unknown in the output and can be omitted in the PFD.
Consider the final part of the example. The liquid stream from the strainer enters a mixer as an input alongside a 700 kg/s stream of club soda. These are the input streams for the final part of the example. The product stream then enters a storage unit. Similar to the first part, the flowrate of the product stream is the sum of the input streams, as shown in Figure 9.
Filter Design Consideration
- Which aspects of the competition ratio are most advantageous (see 2. Water Filter Design and Assembly below)?
- Which materials will filter large sediments out of the contaminated water?
- Which materials will purify the water?
- What order of materials would provide the most cost efficient results?
Materials and Equipment
- A computer with access to the internet
- Materials used in the virtual simulation
- pH strips
- Contaminated water
- Beaker
- Scale
- Alum
- Sodium bicarbonate
- Glass stirring rod
- Sand
- Activated carbon
- Gravel
Price List
| Material | Unit | Cost Per Unit |
|---|---|---|
| Sand | 1 tsp | $1.00 |
| Activated Carbon | 1 tsp | $0.50 |
| Gravel | 1 tsp | $0.25 |
Procedure
The simulation for this lab is done virtually and consists of two parts: pH Neutralization & and Water Filter Assembly.
1. pH Neutralization
- Access the virtual simulation here.
- Immerse one end of the pH strip into the contaminated water.
- Compare the color on the end of the strip to the pH color chart in Figure 4.
- Record the pH and determine if the contaminated water is acidic or alkaline.
- For acidic water, one method of increasing the pH is to add sodium bicarbonate, commonly known as baking soda, which has a pH of approximately 9. If the solution is acidic, add sodium bicarbonate. The general rule of thumb is to add 1 tsp of baking soda per liter of water. Calculate the number of teaspoons of baking soda needed to neutralize the contaminated water.
- Add the baking soda into the contaminated water and mix well.
- Test the pH of the contaminated water again with the pH strips.
- Compare the color on the end of the strip to the pH color chart and record the final pH.
2. Water Filter Design Analysis: Warm-Up Exercise
In this exercise, the relationship between % mass lost and the quantity of each material will be analyzed, given that the quantity of one material is varied at a time for the filter keeping the quantity of other two materials constant. The models are merely approximations and they are not accurate representations of the filter process.
- Download the Lab 8 Data Sheet containing data for this exercise.
- The following steps outline the procedure to create a scatter plot for the sand-varied filter dataset.
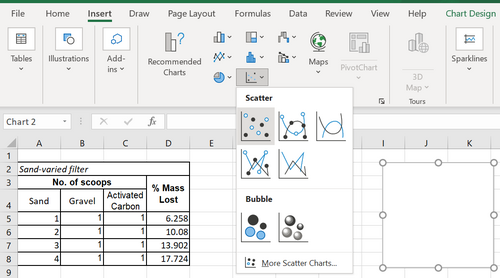
- On the Excel ribbon, click on the Insert tab. Navigate to the Insert Scatter option in the Charts groups and click Scatter. This will create a blank scatter plot as shown in Figure 10.
- Right-click on the empty graph and click Select Data. The Select Data Source dialog box will appear.
- Click Add to add a new dataset to the graph. Enter the series name” % Mass Lost vs Scoops of Sand.
- For Series X values, highlight the cells containing the number of teaspoons of sand from the sand-varied filter dataset (A9:A12). For Series Y values, highlight the % mass lost data for the sand-varied filter (D9:D12).
- Rename the axis and chart titles by clicking the Chart Design tab on the Excel Ribbon, then navigating to Add Chart Element and selecting the appropriate Title option.
- To insert a trendline, select Add Chart Element, then navigate to the Trendline option and select Linear.
- Double click on the newly created trendline. A Format Trendline dialog box will appear on the right side of the Excel window.
- Click on the Trendline options category with the icon that looks like a column chart, as shown in Figure 11. Check off Display Equation on the chart.
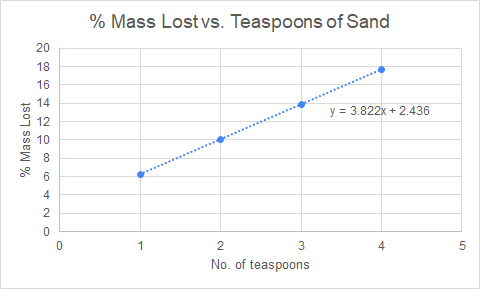
- The finished scatter plot should look like Figure 12.
- On the Excel ribbon, click on the Insert tab. Navigate to the Insert Scatter option in the Charts groups and click Scatter. This will create a blank scatter plot as shown in Figure 10.
- Repeat the above steps to create a scatter plot for the gravel-varied and activated carbon-varied filters.
Pay attention to the linear relationship illustrated by the trendline equation in all three scatter plots. It can be deduced that a filter in which the quantity of all three materials is varied would be represented by a linear model of the form (4).
(4)
In (4), d is the total percent mass lost, a is the teaspoons of sand, b is the teaspoons of gravel, c is the teaspoons of activated carbon, and the constants X, Y, Z correspond to the slope of the trendline for the sand-varied, gravel-varied, and activated-carbon varied filters, respectively.
When data is not provided, as in the tables in this exercise, one can use experimental data to derive the relationship given by (4). The extra credit section at the end of this lab manual focuses on using data from Part 3: Water Filter Design and Assembly to derive and analyze this modeling relationship.
3. Water Filter Design and Assembly
- Access the virtual simulation here.
- Record the data in the Excel datasheet downloaded in Part 2 of this experiment.
- Weigh the empty beaker and record the mass. Maximize the screen if the reading on the scale is not legible.
- Pour 250 mL of the contaminated water into the beaker. Weigh the beaker again and record the mass.
- Calculate the mass of just the contaminated water.
- Add a ½ tsp of alum to the beaker and mix the solution well with the glass stirring rod. Observe what happens to the color and clarity of the solution.
- Weigh the beaker again and calculate the mass of just the solution and the alum.
- Calculate the mass of the alum in the Excel datasheet.
- Based on the available materials in Table 1 and their cost, construct a water filter that will most effectively filter the physical sediments.
- Record the following information in the Excel datasheet:
- Number of teaspoons of each filter material
- Total cost
- Weigh the beaker and calculate the mass of just the filtered water.
- Calculate the percent mass lost using (5) and record it in the datasheet. The percent mass lost normalizes the mass of the physical sediments that is lost from the contaminated water during filtration.
(5)
- Calculate the competition ratio of the filter design using (6). The competition ratio judges the preformance the filter is at removing physical sediments from the contaminated water.
(6)
- Repeat steps 9-13 two more times with two different water filter designs. Record the data for each design in the Excel datasheet.
4. Process Flow Diagram
- Design a simplified industrial water treatment system PFD based on the experiments done in this lab. EG1004 recommends Diagrams.net for creating the PFD. Include:
- pH Neutralization
- Coagulation and flocculation
- Sedimentation
- Filtration
- The design will assume that the initial flow of contaminated water is 1000 kg/s. The contaminated water will flow through the following process units:
- pH Neutralizer
- Mixer
- Filter
- Storage
- Based on the numerical data and the given initial mass flow rate, be sure to add the following:
- Amount of contaminated water entering the system.
- Mass flow rate of alum added to the system.
- Divide the mass of the alum by the mass of the contaminated water to find the flow rate of alum needed for the PFD
- Calculate the mass flow rate of physical sediment removed from the system.
- Calculate the mass flow rate of filtered water leaving the system.
Keep in mind the order of filtration and any other process units needed to logically complete the process flow (for example a mixer after adding the alum). See the PFD example in the Overview section for reference. Be mindful of the mass balance (7).
(7)
The lab work is now complete. Refer to the Assignment section for the instructions to prepare the lab report.
5. Advanced Modeling (Extra Credit)
This part of the experiment uses a virtual simulation to create three water filters made from sand, gravel, and charcoal. To model the effect of each filter material on the percent mass lost (4), which as defined in Part 2 relates the number of teaspoons of each material to the percent mass lost, can be formed. Assume that the relationship is linear and takes the form of (8).
(8)
In (8), d is the percent mass lost, a is the teaspoons of sand, b is the teaspoons of gravel, c is the teaspoons of activated carbon, and X, Y, Z are the corresponding constants being solved for. Use Microsoft Excel to solve this matrix based on the data found in the second procedure.
A matrix is an array of numbers, used to summarize data concisely, making it easier to analyze. Take, for example, the system of equations in (9), (10), and (11).
(9)
(10)
(11)
This equation can be solved manually by solving for one variable in terms of the others and doing a few substitutions. This process can be simplified by rewriting the system using matrices. The matrix in (12) represents the system of equations except the terms have been reordered so that the coefficients of the variables can be extracted.
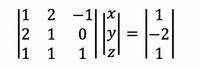
(12)
Thinking of the matrix equation as a regular equation, it would make sense to divide the matrix on the product side by the coefficient matrix, but this is not possible in matrix algebra. The equivalent would be finding the inverse of the coefficient matrix and multiplying that by the product matrix. When a matrix is multiplied by its inverse, the result is the identity matrix that is the matrix equivalent of the value 1 in algebra. When multiplying the product side by the inverse of the coefficient matrix that is dividing one by the other.
It is possible to solve the inverse matrix by hand, but this process can be tedious and time-consuming, especially when there are more than two variables to solve. This part of the experiment will require Excel to solve the system of equations.
In (12), the inverse matrix of the coefficient matrix is calculated to be the matrix in (13) where 1/4 was factored out to make the matrix easier to work with.
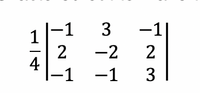
(13)
When the inverse matrix is multiplied by the product matrix, the result is the matrix in (14), where the first value represents x, the second represents y, and the third represents z.
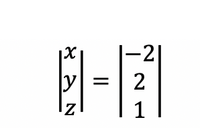
(14)
Using these principles, derive an equation for the value d in terms of the values a, b, and c, using the three equations from the start of this example. Assume the relationship between a, b, c, and d is linear (15).
(15)
In (15), x, y, and z are the coefficient values sought. Thinking about the values of the coefficient matrix as known values of a, b, and c, and the values of the product side as the resultant values of d, use the solution just found to derive the expression (16).
(16)
For this part of the lab, an expression for the %mass lost in terms of the amount of each material (gravel, sand, and activated carbon) will be derived using the data collected in Part 3: Water Filter Design and Assembly. This can be done by hand, but it is more convenient to use matrix properties and Excel to solve the system of equations.
- Using the data collected in Part 2, create three equations, one for every trial, which should be modeled like (15). This will make up the system of equations.
- Let a, b, & c represent the teaspoons of sand, gravel & activated carbon, respectively.
- Let d represent the %Mass Lost for each trial.
- For example, if 1 tsp of sand, 2 tsp of gravel, & 1 tsp of activated carbon were used and there was a 4.5% Mass Lost, the equation would look like .
- Create a coefficient matrix (Matrix A) such that (Figure 13)
- coefficients of x are in the first column
- coefficients of y are in the second column
- coefficients of z are in the third column
- Create a product matrix (Matrix B) that consists of the %Mass Lost values for each trial (Figure 14).
- Find the inverse of Matrix A using Excel’s MINVERSE(array) function, where the array is made up of the values of Matrix A (Cells B1:D3). Note: Before calling the MINVERSE(array) function, highlight the empty cells for the result (Figure 15).
- Solve the system of equations by using Excel’s MMULT(array1, array2) function (Figure 16)
- Array 1 corresponds to the inverse matrix calculated in Step 4.
- Array 2 corresponds to Matrix B created in Step 3.
- The resulting 3x1 matrix represents the values of X, Y, Z
The lab work is now complete. Refer to the Assignment section for the instructions to prepare the lab report.
Assignment
Team Lab Report
Follow the lab report guidelines laid out in the EG1004 Writing Style Guide in the Technical Writing section of the manual. Use the outline below to write this report.
- Describe the water treatment process
- What is pH? Why is it important to maintain the pH of drinking water?
- What was the final pH of the contaminated water?
- What did alum do to the contaminated water? Discuss any observations
- Discuss minimal design. Describe the importance of minimal design and explain how it was employed in the design. Did the design minimize cost?
- Explain the three designs for the water filter, including why certain materials were selected and the order in which they were added
- Compare the three designs. Which was the most cost-effective? Which was the cheapest? Which filtered out the most material?
- Which filter media was the most effective at filtering the contaminated water?
- Explain the thought process behind the PFD designed in Part 3 of the procedure.
- How might the water filter design be improved (both individual and large scale)?
- Include pictures of the water filter, the polluted water, the filtered water, the pH strips, and the complete PFD.
- Discuss what part of the lab each member completed for the group and how it was important to the experiment.
Remember: Lab notes must be taken. Experimental details are easily forgotten unless written down. EG1004 Lab Notes paper can be downloaded and printed from the EG1004 Website. Use the lab notes to write the Procedure section of the lab report. At the end of each lab, a TA will scan the lab notes and upload them to the Lab Documents section of the EG1004 Website. One point of extra credit is awarded if the lab notes are attached at the end of the lab report. Keeping careful notes is an essential component of all scientific practice.
Team Presentation
Follow the presentation guidelines laid out in the EG1004 Lab Presentation Format in the Technical Presentations section of the manual. When preparing the presentation, consider the following points.
- Since one term in the competition ratio is cost, present the cost of the water filter. Use the page How to Show Cost Data in Presentations for instructions on how to do this
- How might the water filter design be improved?
- Include pictures of the water filters, the coagulation and flocculation results, the unfiltered water sample, and the filtered water samples
- Which design was the most cost effective and why?
- Include picture/screenshots of the complete PFD
References
Healthy Water. (2020, March 23). Retrieved July 02, 2020, from https://www.cdc.gov/healthywater
Water Treatment. (2015, January 20). Retrieved July 02, 2020, from https://www.cdc.gov/healthywater/drinking/public/water_treatment.html
FAO's Global Water Information System. Prepared by AQUASTAT, Food and Agriculture Organization of the United Nations, www.fao.org/3/I9253EN/i9253en.pdf.
Guppy, L., Anderson, K., 2017. Water Crisis Report. United Nations University Institute for Water, Environment and Health, Hamilton, Canada.
2018 Edition of the Drinking Water Standards and Health Advisories Tables (2018, March). Retrieved from https://www.epa.gov/sites/production/files/2018-03/documents/dwtable2018.pdf
| ||||||||

![{\displaystyle pH=-log[H^{+}]}](https://wikimedia.org/api/rest_v1/media/math/render/png/085bcfa09edd2b2d817ee499761dc0a43e62817f)


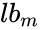 of the upper material and 12
of the upper material and 12 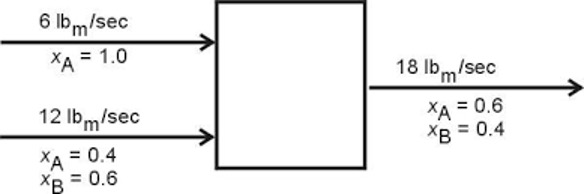

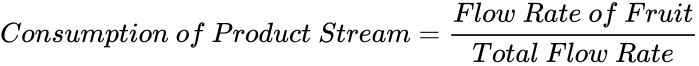
![{\displaystyle Consumption\ of\ Pineapple\ Juice\ Extract={\frac {500\left[{\text{kg/s}}\right]}{675\left[{\text{kg/s}}\right]}}=0.74}](https://wikimedia.org/api/rest_v1/media/math/render/png/b4abdcdde50b0b1e2be3532e4b982d3e22635768)
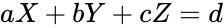
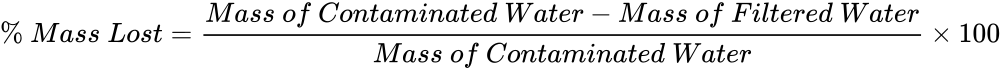
![{\displaystyle Competition\ Ratio={\frac {\%\ Mass\ Lost}{Total\ Cost\left[{\$}\right]}}}](https://wikimedia.org/api/rest_v1/media/math/render/png/b3587795d15335f7dc0fab14a7f6423ed7e76e1b)
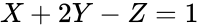
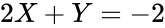
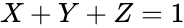
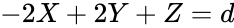
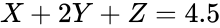 .
.