Difference between revisions of "Boom Construction Competition"
m (→Assignment) |
m (→Assignment) |
||
| Line 179: | Line 179: | ||
=Assignment= | =Assignment= | ||
{{Labs: | {{Labs:Lab Report}} | ||
<ul> | <ul> | ||
Revision as of 16:58, 25 March 2020
Objective
The experimental objective of this lab is to design and construct a boom following the specifications provided. The boom will be entered in a competition against other booms in the section. The competition will be judged by a ratio that uses boom weight and length, weight held, and anchor time. The highest ratio wins.
Overview
A boom is used to lift and move heavy objects, often objects that are much heavier than the boom itself. Distributing the weight of the object, or the load, being lifted over the length of the boom is the main problem in boom design. The design must consider the maximum load the boom will be required to lift, how high the load will be lifted, and whether the boom will be moved or remain stationary while loaded.
Examples of Booms
Certain types of bridges use booms. A cantilever bridge uses two booms extending from a common base. One type of cantilever bridge is a cable-stayed bridge (Figure 1).
The Ed Koch Queensboro Bridge is a double cantilever bridge (Figure 2). It has two bases with two booms extending from each base and the cantilevers placed end to end.
The Grand Bridge over Newtown Creek is a swing bridge, also known as a rotating bridge (Figure 3). This bridge has two booms mounted on a base that rotates.
Figure 4 shows a bascule bridge, more commonly known as a drawbridge, where it is clear that the bridge uses a big, very flat boom.
Not all bridges are booms. Suspension bridges use a deck that is supported by steel cables, not booms. Examples of suspension bridges are the Brooklyn Bridge, Manhattan Bridge, Verrazano-Narrows Bridge, and the George Washington Bridge.
Cranes are the most common example of booms. The crane pictured in Figure 5 is a tower crane. These cranes are a fixture on construction sites around the world. A tower crane can lift a 40,000-pound load. It is attached to the ground by anchor bolts driven through a 400,000-pound concrete pad poured a few weeks before the crane is erected (Howstuffworks.com, 2003).
Stress and Strain
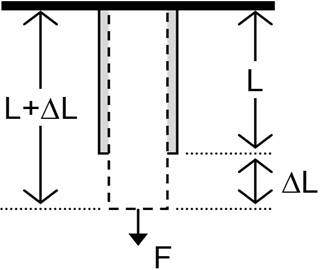
The design of a boom must consider the properties of the materials used to build the boom. The mechanical properties and deformation of solids are explained by stress and strain. When an external force is applied to a material, it changes shape (e.g. changes length and cross-section perpendicular to the length). Understanding how deformation will affect materials is a critical consideration in boom design.
According to Serway and Beichner in “Physics for Scientists and Engineers,” stress is the external force acting on an object per unit cross sectional area. Strain is the measure of deformation resulting from an applied stress (Figure 6).
The expression (1) for tensile stress shows the relationship between an applied force and the cross-sectional area.
(1)
In (1), σ is the stress, F is the applied force, and A is the cross-sectional area of the object perpendicular to the force. The resulting strain (2) is calculated by dividing the change in length of the object by the original length.
(2)
In (2), ΔL is the change in length and L0 is the object's original length.
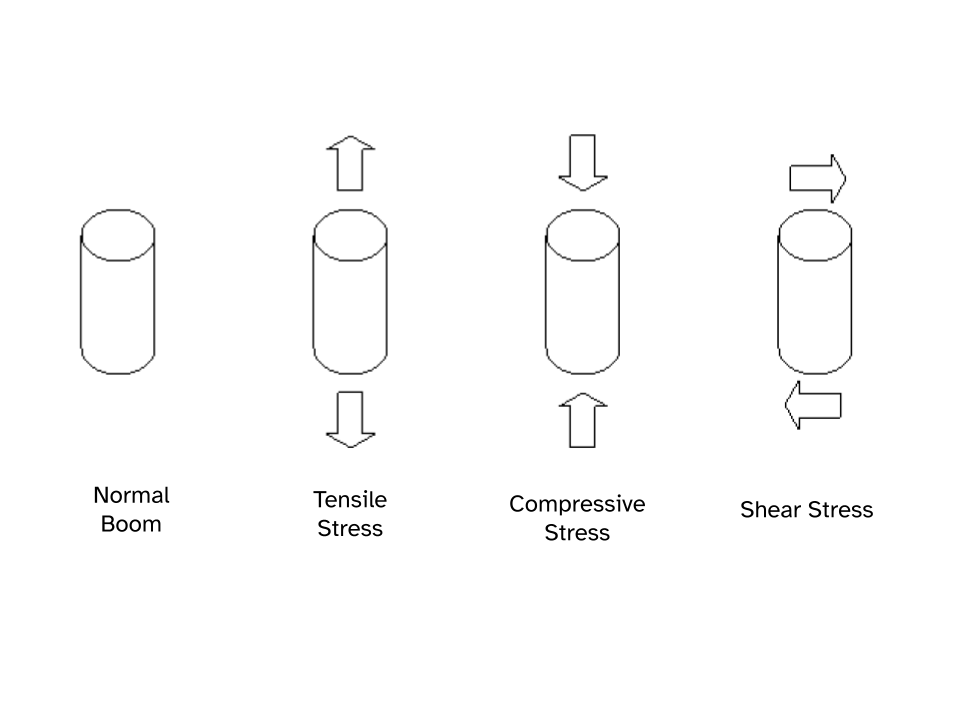
There are three basic types of stresses; tensile (pulling or stretching), compressive (squeezing or squashing), and shear (bending or cleaving). If a rod of material is put under tensile stress, its length increases slightly in the direction of the applied force and its cross-section perpendicular to the force decreases. If the rod is placed under compressive stress, its length in the direction of the force will decrease and its cross-section perpendicular to the force will increase. If the rod is place under shear stress, it will bend in the direction of the applied force and its length and cross-section will be distorted (Figure 7).
Strain is proportional to stress for small values of strain. The proportionality constant depends on the material being deformed and on the type of deformation. The proportionality constant is called the elastic modulus, or Young’s modulus. The moduli for different materials vary considerably and the various moduli for a particular material may also vary significantly. Concrete, for example, is very strong in compression, but less so in tension, and wood breaks quite easily when bent because its natural grain is anisotropic (properties depend on the direction of the material).
Stress-Strain Curve
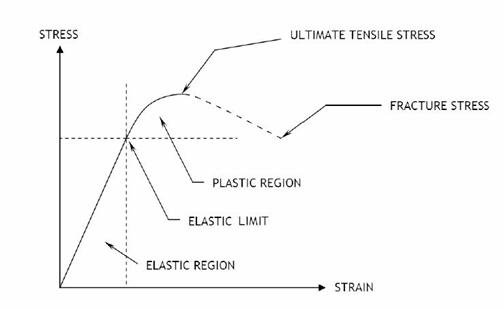
A stress-strain curve graphically shows the relationship between the stress and strain of a material under load (Figure 8). In the elastic region, the material will regain its original shape once the stress or load is removed. In the plastic region, the material loses its elasticity and is permanently deformed.
The elastic limit for a material is the maximum strain it can sustain before it becomes permanently deformed (i.e. if the stress is decreased, the object no longer returns to its original size and shape). If the stress is greater than the elastic limit, the material will plastically deform and for sufficiently large stress ultimately fail. The ultimate tensile strength is the maximum stress a material can undergo. The fracture stress is the point at which the material breaks under tension. Fracture stress is lower than the ultimate tensile strength because as strain increases, the material becomes thinner and thinner. As this necking down process continues, the load that can be supported decreases and the material breaks.
In addition to these intrinsic materials factors, the behavior of materials as they age and are used in service must be considered in boom design. These factors do not relate directly to the boom design in this lab, but they must be considered when deciding what material to use for an actual design. The loss of desirable properties through use, called fatigue, is important. Non-static loads, repeated loading and unloading, or loads that include vibrations or oscillations may lead to failure in service. Special care must be taken with live loads and situations where small motions may be magnified by design features.
There are many factors to consider in any design project. When designing and constructing the boom for this competition, remember to consider the materials being used and what might cause those materials to fail under a load.
Competition Rules
The competition rules must be followed at all times during the competition. Violation of any of these rules will result in the disqualification of the design.
- The boom is to be secured (i.e. anchored) to the white plastic anchorage provided at the front of the lab
- The boom must extend at least 1.5 meters horizontally from the front edge of the anchorage
- The boom must be anchored in two minutes or less
- The boom may not touch anything but the anchorage
- The basic weight ratio (3) for the competition uses the weight supported divided by the boom weight
- The winning design will be determined by the weighted design ratio (4), which uses the weight ratio, anchor time, and boom length
(3)
(4)
Design Considerations
- Which aspects of the competition ratio are most advantageous?
- How can the boom be built and/or reinforced to prevent as much deflection as possible?
Materials and Equipment
- Two thick dowels (1.1 cm × 122 cm)
- Two thin dowels (0.8 cm × 122 cm)
- Six bamboo skewers (30.5 cm)
- 3D printed dowel connectors
- Cellophane tape
- Kevlar string
Note: A saw is available to cut the dowels. Ask a TA for assistance, as only TAs may use the saw.
Procedure
Boom Design and Construction
- Assess the materials and consider the design options, keeping in mind the competition specifications. Preliminary sketches must be completed during this process
- Sketch the basic design in pencil using the lab notes paper provided by a TA or on the EG1003 website. Label the design clearly and have a TA sign and date it
- Construct the boom based on the completed sketch and the available materials. A TA will provide the materials allowed for the design. If the design is modified during the construction phase, make sure to note the changes and describe the reasons for them
- A TA will weigh the boom and record the weight in the competition spreadsheet for the section
Competition
Note: Attaching the boom to the anchorage is a critical phase of the competition. Anchoring will be timed. Making sure there is a plan to anchor the boom quickly will improve its standing in the competition. Practice anchoring before the trial begins. The boom will be disqualified if anchoring the boom takes more than two minutes.
- When the TA says "go," attach the boom to the anchorage and shout "done" when the boom is anchored. The TA will only stop the timer once there are no more hands touching the boom. The TA will give the anchoring time. This value will be used to compute the boom's design ratio
- A TA will measure the boom and record the length in the competition spreadsheet for the section
- A TA will attach a basket to the end of the boom and add weights until the boom deflects (bends) 0.2 m vertically. The load supported will be weighed on the lab scale and recorded in the competition spreadsheet for the section (Figure 10)
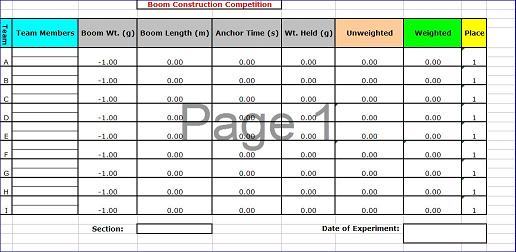
A TA has prepared an Excel file with the section's results. It can be accessed in the Lab Documents section of the EG1003 website. This chart must be included in the PowerPoint presentation and in the Data/Observations section of the lab report. The lab work is now complete. Please clean up the workstation. Return all unused materials to a TA. Refer to the Assignment section for the instructions to prepare the lab report.
Assignment
Follow the lab report guidelines laid out in the EG1004 Writing Style Guide in the Technical Writing section of the manual. Use the outline below to write this report.
- Describe the rules of the competition in the Introduction. What consequences did the rules have for any design decisions? Use the appropriate equations in the answer.
- What factors were considered in designing the boom? Was any of the background information used?
- What was the basic weight ratio and weighted design ratio for the design?
- Describe how the components chosen functioned in the design, and describe its height/length/shape
- Describe the advantages and disadvantages of the boom design
- Discuss design improvements. How can the design be optimized (i.e. improve the ratio) based on experience?
- Which elements of the boom (e.g., wooden dowels, 3D printed dowel connectors, Kevlar string, etc.,) were stressed by the load, in what directions, and contributed to the failure?
- Include the spreadsheet with every boom's results. Describe the results and talk about other designs in the class
Remember: Lab notes must be taken. Experimental details are easily forgotten unless written down. EG1004 Lab Notes paper can be downloaded and printed from the EG1004 Website. Use the lab notes to write the Procedure section of the lab report. At the end of each lab, a TA will scan the lab notes and upload them to the Lab Documents section of the EG1004 Website. One point of extra credit is awarded if the lab notes are attached at the end of the lab report. Keeping careful notes is an essential component of all scientific practice.
Team PowerPoint Presentation
Follow the presentation guidelines laid out in the EG1004 Lab Presentation Format in the Technical Presentations section of the manual. When preparing the presentation, consider the following points.
- How can the boom design be improved?
- Other than the examples given in this lab, what are other examples of booms?
- Which elements of the boom (e.g., wooden dowels, 3D printed dowel connectors, Kevlar string, etc.,) were stressed by the load, in what directions, and contributed to the failure?
References
How Stuff Works website. 2003. SHW Media Network. Retrieved July 28, 2003. http://science.howstuffworks.com/tower-crane3.htm
Jennings, James. 2015. “Up, UP in a Crane: What Life is Like as a Tower Crane Operator.” Philadelphia. Accessed 14 January 2020 from www.phillymag.com
Serway, R., Beichner, R., Physics for Scientists and Engineers with Modern Physics, 5th Edition. Fort Worth, TX: Saunders College Publishing, 2000
| ||||||||





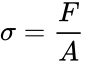
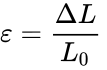
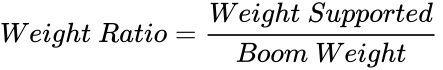
![{\displaystyle Design\ Ratio={\frac {Weight\ Supported}{Boom\ Weight}}\times {\frac {60\left[{\text{s}}\right]}{Anchor\ Time\left[{\text{s}}\right]+30\left[{\text{s}}\right]}}\times {\frac {Boom\ Length\left[{\text{m}}\right]}{1.5\left[{\text{m}}\right]}}\,}](https://wikimedia.org/api/rest_v1/media/math/render/png/813810ebf568ed2a63b9be2be614b546aeff20fa)