Difference between revisions of "Boom Construction Competition (Virtual)"
(1003 --> 1004) |
|||
| (13 intermediate revisions by 3 users not shown) | |||
| Line 2: | Line 2: | ||
The experimental objective of this lab is to design and construct a boom in Fusion 360 following the specifications provided. The boom will be entered in a competition against other booms in the section. The designs will be judged by a competition ratio that uses boom mass, boom length, and the generated reaction force while deflecting 20 cm. The design with the highest competition ratio wins. | The experimental objective of this lab is to design and construct a boom in Fusion 360 following the specifications provided. The boom will be entered in a competition against other booms in the section. The designs will be judged by a competition ratio that uses boom mass, boom length, and the generated reaction force while deflecting 20 cm. The design with the highest competition ratio wins. | ||
= Overview = | =Overview= | ||
A <b>boom</b> is used to lift and move heavy objects, often objects that are much heavier than the boom itself. Distributing the weight of the object, or the load, being lifted over the length of the boom is the main problem in boom design. The design must consider the load the boom will be required to lift, how high the load will be lifted, and whether the boom will | |||
A <b>boom</b> is used to lift and move heavy objects, often objects that are much heavier than the boom itself. Distributing the weight of the object, or the load, being lifted over the length of the boom is the main problem in boom design. The design must consider the maximum load the boom will be required to lift, how high the load will be lifted, and whether the boom will be moved or remain stationary while loaded. | |||
== Examples of Booms == | == Examples of Booms == | ||
Certain types of bridges use booms. A cantilever bridge uses two booms extending from a common base. One type of cantilever bridge is a cable-stayed bridge (Figure 1). | Certain types of bridges use booms. A cantilever bridge uses two booms extending from a common base. One type of cantilever bridge is a cable-stayed bridge (Figure 1). | ||
[[Image:Lab_boom_13.png|650px|thumb|center|Figure 1: A Cable-Stayed (Cantilever) Bridge]] | [[Image:Lab_boom_13.png|650px|thumb|center|Figure 1: A Cable-Stayed (Cantilever) Bridge]] | ||
| Line 15: | Line 17: | ||
The Grand Bridge over Newtown Creek is a swing bridge, also known as a rotating bridge (Figure 3). This bridge has two booms mounted on a base that rotates. | The Grand Bridge over Newtown Creek is a swing bridge, also known as a rotating bridge (Figure 3). This bridge has two booms mounted on a base that rotates. | ||
[[Image:lab_boom_11.jpg|650px|thumb|center|Figure 3: Grand Bridge (Swing Bridge)]] | [[Image:lab_boom_11.jpg|650px|thumb|center|Figure 3: Grand Bridge (Swing Bridge)]] | ||
Figure 4 shows a bascule bridge, more commonly known as a drawbridge, where it is clear that the bridge uses a big, very flat boom. | Figure 4 shows a bascule bridge, more commonly known as a drawbridge, where it is clear that the bridge uses a big, very flat boom. | ||
[[Image:lab_boom_12.jpg|650px|thumb|center|Figure 4: Bascule Bridge]] | [[Image:lab_boom_12.jpg|650px|thumb|center|Figure 4: Bascule Bridge]] | ||
Not all bridges are booms. Suspension bridges use a deck that is supported by steel cables, not booms. Examples of suspension bridges are the Brooklyn Bridge, Manhattan Bridge, Verrazano-Narrows Bridge, and the George Washington Bridge. | Not all bridges are booms. Suspension bridges use a deck that is supported by steel cables, not booms. Examples of suspension bridges are the Brooklyn Bridge, Manhattan Bridge, Verrazano-Narrows Bridge, and the George Washington Bridge. | ||
Cranes are the most common example of booms. The crane pictured in Figure 5 is a tower crane. These cranes are a fixture on construction sites around the world. A tower crane can lift a 40,000-pound load. It is attached to the ground by anchor bolts driven through a 400,000-pound concrete pad poured a few weeks before the crane is erected (Howstuffworks.com, 2003). | Cranes are the most common example of booms. The crane pictured in Figure 5 is a tower crane. These cranes are a fixture on construction sites around the world. A tower crane can lift a 40,000-pound load. It is attached to the ground by anchor bolts driven through a 400,000-pound concrete pad poured a few weeks before the crane is erected (Howstuffworks.com, 2003). | ||
[[Image:Tower Crane.jpg|650px|thumb|center|Figure 5: A Tower Crane (Jennings, 2015)]] | [[Image:Tower Crane.jpg|650px|thumb|center|Figure 5: A Tower Crane (Jennings, 2015)]] | ||
| Line 33: | Line 36: | ||
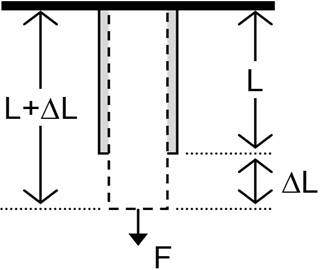
According to Serway and Beichner in “Physics for Scientists and Engineers,” <b>stress</b> is the external force acting on an object per unit cross sectional area. <b>Strain</b> is the measure of deformation resulting from an applied stress (Figure 6). | According to Serway and Beichner in “Physics for Scientists and Engineers,” <b>stress</b> is the external force acting on an object per unit cross sectional area. <b>Strain</b> is the measure of deformation resulting from an applied stress (Figure 6). | ||
[[Image:lab_boom_1.jpg|frame|center|Figure 6: Material Under Tension]] | [[Image:lab_boom_1.jpg|frame|center|Figure 6: Material Under Tension]] | ||
| Line 40: | Line 42: | ||
<center><math>\sigma = \frac{F}{A}\,</math></center> | <center><math>\sigma = \frac{F}{A}\,</math></center> | ||
<p style="text-align:right">(1)</p> | <p style="text-align:right">(1)</p> | ||
In (1), σ is the stress, F is the applied force, and A is the cross-sectional area of the object perpendicular to the force. The resulting strain (2) is calculated by dividing the change in length of the object by the original length. | In (1), σ is the stress, F is the applied force, and A is the cross-sectional area of the object perpendicular to the force. The resulting strain (2) is calculated by dividing the change in length of the object by the original length. | ||
<center><math>\varepsilon = \frac{\Delta L}{L_{\text{0}}}\,</math></center> | <center><math>\varepsilon = \frac{\Delta L}{L_{\text{0}}}\,</math></center> | ||
<p style="text-align:right">(2)</p> | <p style="text-align:right">(2)</p> | ||
| Line 48: | Line 50: | ||
In (2), ΔL is the change in length and L<sub>0</sub> is the object's original length. | In (2), ΔL is the change in length and L<sub>0</sub> is the object's original length. | ||
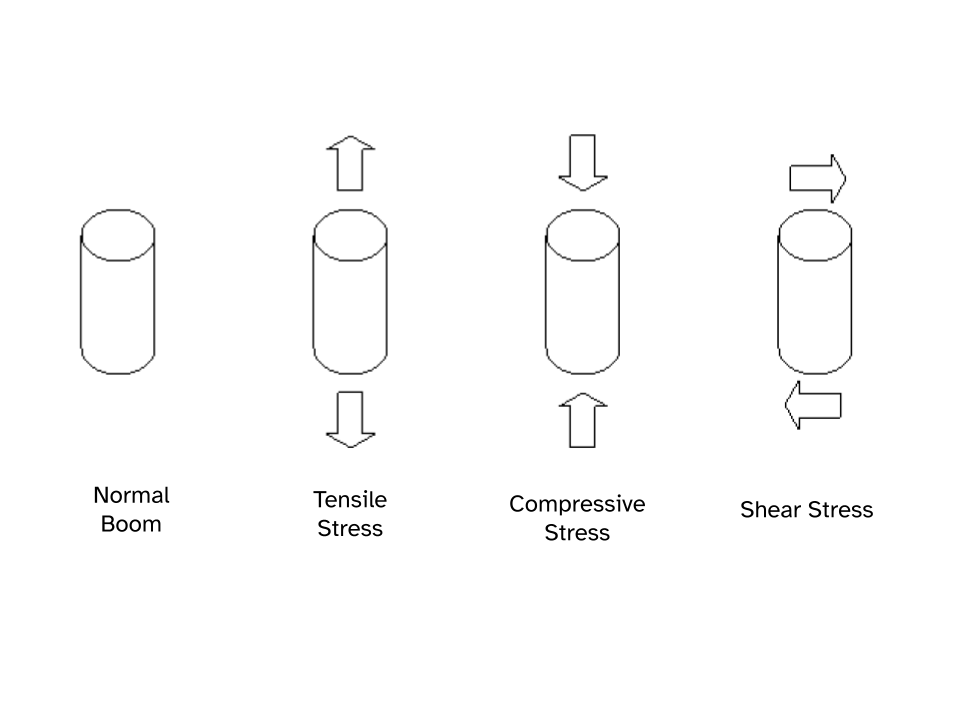
There are three basic types of stresses; tensile (pulling or stretching), compressive (squeezing or squashing), and shear (bending or cleaving). If a | There are three basic types of stresses; <b>tensile</b> (pulling or stretching), <b>compressive</b> (squeezing or squashing), and <b>shear</b> (bending or cleaving). Consider a straight metal beam. If a <b>tensile stress</b> is applied to both ends, its length will increase in both directions of the force, while its cross-sectional area perpendicular to the force applied will decrease. Under <b>compressive stress</b>, the opposite will occur. If the beam is subjected to <b>shear stress</b>, it will bend towards the direction of the applied force, and both the length and cross-sectional area of the beam will become distorted. Figure 7 depicts a graphic representation of the three common forms of stress. | ||
[[Image:Lab_boom_7.gif|frame|center|Figure 7: Example of Cylindrical Material Under Three Common Modes of Stress]] | |||
Strain is proportional to stress for material dependent values of strain. If the material is known, it is possible to derive strain from measured stress, and vice-versa, up to a certain level of stress. This unitless mathematical constant is referred to as the elastic modulus, or Young’s modulus. The moduli of different materials is an important factor to consider when designing or building any form of structure meant to encounter stresses. | |||
== Stress-Strain Curve == | == Stress-Strain Curve == | ||
A <b>stress-strain | A <b>stress-strain</b> curve graphically shows the relationship between the stress and strain of a material under load. Figure 8 shows the stress-strain curve of a common metallic building material. In the elastic region, the material will regain its original shape once the stress or load is removed. Note that the <b>elastic region</b> in Figure 8 is fairly linear. The slope of this linear portion of the stress-strain curve is the elastic modulus, as defined above. | ||
[[Image:lab_boom_2.jpg|frame|center|Figure 8: Stress-Strain Curve of a Material Under Tension]] | [[Image:lab_boom_2.jpg|frame|center|Figure 8: Stress-Strain Curve of a Material Under Tension]] | ||
The <b>elastic limit</b> for a material is the maximum strain it can sustain before it becomes permanently deformed (i.e. if the stress is decreased, the object no longer returns to its original size and shape). | The <b>elastic limit</b> for a material is the maximum strain it can sustain before it becomes permanently deformed (i.e. if the stress is decreased, the object no longer returns to its original size and shape). In the <b>plastic region</b>, the material loses its elasticity and is permanently deformed. A linear approximation with the elastic modulus is no longer accurate. | ||
In addition to these intrinsic | The <b>ultimate tensile strength</b> is the maximum stress a material can undergo. The <b>fracture stress</b> is the point at which the material breaks. Fracture stress is lower than the ultimate tensile strength of a material as by the time a material reaches that level of stress, it has already begun to rip apart. Thus, the cross-sectional area is constantly decreasing until the material finally breaks. | ||
There are many factors to consider in any design project. When designing and constructing the boom for this competition, consider the materials being used and what might cause those materials to fail under a load. | |||
In addition to these intrinsic materials factors, the behavior of materials as they age and are used in service must be considered in boom design. These factors do not relate directly to the boom design in this lab, but they must be considered when deciding what material to use for an actual design. The loss of desirable properties through use, called <b>fatigue</b>, is important. Non-static loads, repeated loading and unloading, or loads that include vibrations or oscillations will eventually lead to failure in service. Special care must be taken with live loads and situations where small motions may be magnified by design features. | |||
<!--<p>The first aging factor is chemical degradation and, in particular, <b><i>corrosion</i></b>. Light and | |||
chemicals present in the | |||
environment can cause chemical reactions with the materials chosen for a | |||
design. These reactions can cause a loss | |||
of strength, flexibility or other desirable material properties. Corrosion | |||
occurs when two or more materials or substances react with each other, in the | |||
presence of an electrolyte. For example, | |||
rust results when iron or simple steel is exposed to water, or just even humid | |||
air. Rust is particularly damaging | |||
because it flakes off, thinning and weakening the underlying material. Careful choice of material will minimize the effects of chemical degradation. However, | |||
the cost is often limiting factor and cheap countermeasures like paint and other | |||
coatings are often employed.</p> | |||
<p><b><i>Erosion</i></b> is another | |||
factor in material failure. It is weathering caused by exposure to | |||
environmental factors like wind driven dust or sand, rain or flowing water. The | |||
smoothing of rocks by a river or the sea is a good example of this kind of | |||
process. Care in the design process can | |||
help minimize the effect of erosion. | |||
Again the cost is often the limiting factor and coatings are often employed | |||
to protect an object.</p> | |||
<p>A third factor in material failure is <b><i>thermal | |||
cycling</i></b>. Materials in an object | |||
will routinely warm up and cool down while in use (especially device that | |||
generates heat internally), over the course of a normal day, or even over a | |||
year. This thermal cycling is | |||
accompanied by physical expansion and contraction of the object. Different materials expand and contract by | |||
different amounts and this can lead to internal stress and strains, and | |||
ultimately failure. Careful choice and | |||
matching of materials can minimize the effects of thermal cycling, but the cost may | |||
limit the choices. Accumulations of | |||
water, which can freeze and thaw, can be very damaging and coatings are often | |||
especially vulnerable to thermal cycling as they may crack and peel off, | |||
exposing the underlying material in need of protection.</p> | |||
<p>A related but more dramatic mode of failure is <b><i>thermal shock</i></b>. | |||
This can occur when objects made of certain | |||
materials are exposed to extreme temperature changes over a short period of | |||
time. If the material is inhomogeneous | |||
(i.e., properties not uniform throughout), thermal expansion or contraction can | |||
be sufficiently non-uniform to cause cracking. | |||
If the cracks spread far enough, the material will fail in spectacular | |||
fashion. Imagine quickly immersing a | |||
very cold ordinary glass bottle in very hot water. Often such failures can be avoided by heat | |||
treatment (annealing) and in general, material properties can be improved | |||
significantly through heat treatment and mechanical working. For example, the familiar Pyrex<sup>TM</sup> | |||
glass is specially treated to avoid thermal shock.</p>--> | |||
There are many factors to consider in any design project. When designing and constructing the boom for this competition, remember to consider the materials being used and what might cause those materials to fail under a load. | |||
== Simulations == | == Simulations == | ||
An important tool in an engineer’s skillset is the use of | An extremely important tool in an engineer’s skillset is the use of simulation tools. Many times, complex designs require quick analysis that cannot be done by calculation or prototyping, so simulation comes in handy and as it saves both time and money. Specifically, <b>Finite Element Analysis (FEA)</b> is a process that a computer software undergoes to simulate a desired scenario. The software calculates mathematical formulas at hundreds to thousands of points on a design, referred to as a mesh, and computes them simultaneously to get a complete look at what would happen. This simulation only works for isotropic materials, meaning that the materials properties (tensile strengths, modulus, etc.) are the same for all sides of the material. This may not be true for certain materials, and an engineer must take this into account. While members of the group are designing and building a boom, others will simulate a basic design in order to understand the effect of the forced displacement, and use that information to improve the initial design. | ||
== Fusion 360 == | == Fusion 360 == | ||
| Line 144: | Line 197: | ||
== 2. Importing Parts == | == 2. Importing Parts == | ||
# The parts for the boom can be found in a ZIP folder [[Media: | # The parts for the boom can be found in a ZIP folder [[Media: Boom_Parts.zip|here]]. The latest version of Fusion 360 must be downloaded for the parts to appear properly. | ||
# Unzip the parts to a space on the computer. | # Unzip the parts to a space on the computer. | ||
# In Fusion 360, open the Data Panel (icon with 9 boxes at the top left) and click Upload. Select the unzipped part files to upload them to Fusion 360’s cloud memory (Figure 14). Fusion 360 can only import files uploaded to its cloud. | # In Fusion 360, open the Data Panel (icon with 9 boxes at the top left) and click Upload. Select the unzipped part files to upload them to Fusion 360’s cloud memory (Figure 14). Fusion 360 can only import files uploaded to its cloud. | ||
| Line 161: | Line 214: | ||
=== Mass of the Boom === | === Mass of the Boom === | ||
# Go to the Browser on the left-hand side of the workspace. | # After completing the model of the boom in Fusion 360, switch the workspace from Design to Simulation at the top left of the screen. In the New Study dialog that appears, select Static Stress > Create Study. | ||
# Go to the Browser on the left-hand side of the Simulation workspace. Right click 'Simulation Model 1' and select Properties (Figure 16). | |||
# In the Properties dialog that appears, record the mass of the body. | # In the Properties dialog that appears, record the mass of the body. | ||
[[Image:Bc11.png|600px|thumb|center|Figure 16: Obtain Mass of Bodies]] | [[Image:Bc11.png|600px|thumb|center|Figure 16: Obtain Mass of Bodies]] | ||
| Line 175: | Line 228: | ||
== 5. Simulate the Boom == | == 5. Simulate the Boom == | ||
# | |||
# Make sure that you are in the Simulation workspace. The Simulation toolbar in Fusion 360 lays out the steps from left to right that must be taken to fully run a simulation (Figure 18). [[Image:Bc13.png|750px|thumb|center|Figure 18: Simulation Toolbar]] | |||
# To study and change the type of material, in the Simulation toolbar go to Materials > Study Materials. | # To study and change the type of material, in the Simulation toolbar go to Materials > Study Materials. | ||
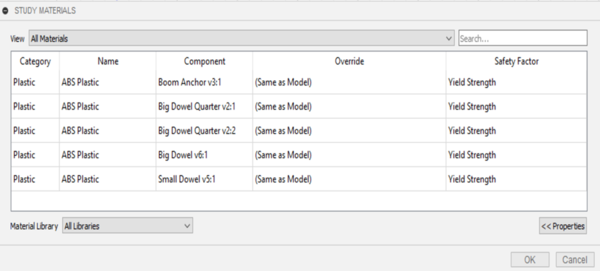
# In the Study Materials dialog, ensure all the parts have ABS plastic as their material, including the dowels (Figure 19). Click OK. Note: ABS is the most commonly used plastic and an isotropic material, meaning its material properties are the same in all directions. This is why running simulations on wood, which is orthotropic (directional) based on grain, is mathematically more difficult.[[Image:Bc14.png|600px|thumb|center|Figure 19: Study Materials Dialog]] | # In the Study Materials dialog, ensure all the parts have ABS plastic as their material, including the dowels (Figure 19). Click OK. <font color="red">'''Note: ABS is the most commonly used plastic and an isotropic material, meaning its material properties are the same in all directions. This is why running simulations on wood, which is orthotropic (directional) based on grain, is mathematically more difficult.'''</font>[[Image:Bc14.png|600px|thumb|center|Figure 19: Study Materials Dialog]] | ||
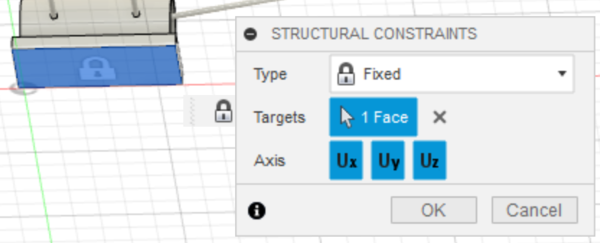
# To ensure that the boom is not floating in free space and that the load will be properly applied to the boom, a fixed face must be added. In the Simulation toolbar, go to Constraints > Structural Constraints. | # To ensure that the boom is not floating in free space and that the load will be properly applied to the boom, a fixed face must be added. In the Simulation toolbar, go to Constraints > Structural Constraints. | ||
# Select the bottom face of the anchor as the Targets. Ensure the Type of constraint is Fixed. The Structural Constraints dialog should look like Figure 20. Click OK.[[Image:Bc15.png|600px|thumb|center|Figure 20: Structural Constraints]] | # Select the bottom face of the anchor as the Targets. Ensure the Type of constraint is Fixed. The Structural Constraints dialog should look like Figure 20. Click OK.[[Image:Bc15.png|600px|thumb|center|Figure 20: Structural Constraints]] | ||
| Line 193: | Line 246: | ||
== 6. Interpret the Results == | == 6. Interpret the Results == | ||
# After the simulation has been solved, the workspace will show a deflected boom similar to the one shown below in Figure 23. | # After the simulation has been solved, the workspace will show a deflected boom similar to the one shown below in Figure 23. | ||
# The scale on the right displays the Safety Factor, which can range from | # The scale on the right displays the Safety Factor, which can range from 0-15. Make sure the minimum safety factor is above 1. | ||
# If the safety factor is below 1 anywhere other than the tip of the boom, the materials have failed. Check for the areas of discrepancy, making sure the contacts and the displacement are set properly, and run the simulation again. If this persists, state that the simulation had a safety factor of less than 1 and the materials failed.[[Image:Bc18.png|600px|thumb|center|Figure 23: Sample Boom Deflection]] | # If the safety factor is below 1 anywhere other than the tip of the boom, the materials have failed. Check for the areas of discrepancy, making sure the contacts and the displacement are set properly, and run the simulation again. If this persists, state that the simulation had a safety factor of less than 1 and the materials failed.[[Image:Bc18.png|600px|thumb|center|Figure 23: Sample Boom Deflection]] | ||
# The boom should be straight and deflect downward relatively evenly. If the boom does not look like the boom shown in Figure 23, increase the tolerance of the contacts by creating another set of Automatic Contacts. Ensure the boom is deflecting downwards and on no other axis, and that the deformation is set on Actual (Results toolbar > Deformation > Actual). Ensure the Reactions are being observed (Results toolbar > Inspect > Reactions). The toolbar should look like Figure 24. The maximum reaction force and point of failure may be at the tip of the boom. This is fine and merely a consequence of the mesh. | # The boom should be straight and deflect downward relatively evenly. If the boom does not look like the boom shown in Figure 23, increase the tolerance of the contacts by creating another set of Automatic Contacts. Ensure the boom is deflecting downwards and on no other axis, and that the deformation is set on Actual (Results toolbar > Deformation > Actual). Ensure the Reactions are being observed (Results toolbar > Inspect > Reactions). The toolbar should look like Figure 24. The maximum reaction force and point of failure may be at the tip of the boom. This is fine and merely a consequence of the mesh. | ||
| Line 207: | Line 260: | ||
[[Image:lab_boom_5.jpg|frame|center|Figure 26: Sample Competition Spreadsheet]] | [[Image:lab_boom_5.jpg|frame|center|Figure 26: Sample Competition Spreadsheet]] | ||
<p>Give the length, mass, and reaction force of the boom design to a Lab TA. The Lab TAs have prepared an Excel file with the section's competition results. It can be accessed in the [http://eg.poly.edu/documents.php Lab Documents] section of the | <p>Give the length, mass, and reaction force of the boom design to a Lab TA. The Lab TAs have prepared an Excel file with the section's competition results. It can be accessed in the [http://eg.poly.edu/documents.php Lab Documents] section of the EG1004 website. This chart must be included in the PowerPoint presentation and in the Data/Observations section of the lab report. All competition labs will include a competition scoresheet for the section that will be referenced to in the assignment. | ||
Take a screenshot of the designed boom and send it to the Lab TA. The lab work is now complete. Refer to the Assignment section for the instructions needed to prepare the lab report. | Take a screenshot of the designed boom and send it to the Lab TA. The lab work is now complete. Refer to the Assignment section for the instructions needed to prepare the lab report. | ||
| Line 214: | Line 267: | ||
== Individual Lab Report == | == Individual Lab Report == | ||
{{Ambox | |||
| type = notice | |||
| text = <h4>Extra Credit Opportunity</h4>Students who perform well on this report have the opportunity to replace a lower score on an earlier lab report with their score on this report.}} | |||
{{Labs:Lab Report}} | {{Labs:Lab Report}} | ||
| Line 245: | Line 303: | ||
Serway, R., Beichner, R., Physics for Scientists and Engineers with Modern Physics, 5th Edition. Fort Worth, TX: Saunders College Publishing, 2000 | Serway, R., Beichner, R., Physics for Scientists and Engineers with Modern Physics, 5th Edition. Fort Worth, TX: Saunders College Publishing, 2000 | ||
{{Laboratory Experiments}} | |||
Latest revision as of 18:22, 22 August 2022
Objective
The experimental objective of this lab is to design and construct a boom in Fusion 360 following the specifications provided. The boom will be entered in a competition against other booms in the section. The designs will be judged by a competition ratio that uses boom mass, boom length, and the generated reaction force while deflecting 20 cm. The design with the highest competition ratio wins.
Overview
A boom is used to lift and move heavy objects, often objects that are much heavier than the boom itself. Distributing the weight of the object, or the load, being lifted over the length of the boom is the main problem in boom design. The design must consider the maximum load the boom will be required to lift, how high the load will be lifted, and whether the boom will be moved or remain stationary while loaded.
Examples of Booms
Certain types of bridges use booms. A cantilever bridge uses two booms extending from a common base. One type of cantilever bridge is a cable-stayed bridge (Figure 1).
The Ed Koch Queensboro Bridge is a double cantilever bridge (Figure 2). It has two bases with two booms extending from each base and the cantilevers placed end to end.
The Grand Bridge over Newtown Creek is a swing bridge, also known as a rotating bridge (Figure 3). This bridge has two booms mounted on a base that rotates.
Figure 4 shows a bascule bridge, more commonly known as a drawbridge, where it is clear that the bridge uses a big, very flat boom.
Not all bridges are booms. Suspension bridges use a deck that is supported by steel cables, not booms. Examples of suspension bridges are the Brooklyn Bridge, Manhattan Bridge, Verrazano-Narrows Bridge, and the George Washington Bridge.
Cranes are the most common example of booms. The crane pictured in Figure 5 is a tower crane. These cranes are a fixture on construction sites around the world. A tower crane can lift a 40,000-pound load. It is attached to the ground by anchor bolts driven through a 400,000-pound concrete pad poured a few weeks before the crane is erected (Howstuffworks.com, 2003).
Stress and Strain
The design of a boom must consider the properties of the materials used to build the boom. The mechanical properties and deformation of solids are explained by stress and strain. When an external force is applied to a material, it changes shape (e.g. changes length and cross-section perpendicular to the length). Understanding how deformation will affect materials is a critical consideration in boom design.
According to Serway and Beichner in “Physics for Scientists and Engineers,” stress is the external force acting on an object per unit cross sectional area. Strain is the measure of deformation resulting from an applied stress (Figure 6).
The expression (1) for tensile stress shows the relationship between an applied force and the cross-sectional area.
(1)
In (1), σ is the stress, F is the applied force, and A is the cross-sectional area of the object perpendicular to the force. The resulting strain (2) is calculated by dividing the change in length of the object by the original length.
(2)
In (2), ΔL is the change in length and L0 is the object's original length.
There are three basic types of stresses; tensile (pulling or stretching), compressive (squeezing or squashing), and shear (bending or cleaving). Consider a straight metal beam. If a tensile stress is applied to both ends, its length will increase in both directions of the force, while its cross-sectional area perpendicular to the force applied will decrease. Under compressive stress, the opposite will occur. If the beam is subjected to shear stress, it will bend towards the direction of the applied force, and both the length and cross-sectional area of the beam will become distorted. Figure 7 depicts a graphic representation of the three common forms of stress.
Strain is proportional to stress for material dependent values of strain. If the material is known, it is possible to derive strain from measured stress, and vice-versa, up to a certain level of stress. This unitless mathematical constant is referred to as the elastic modulus, or Young’s modulus. The moduli of different materials is an important factor to consider when designing or building any form of structure meant to encounter stresses.
Stress-Strain Curve
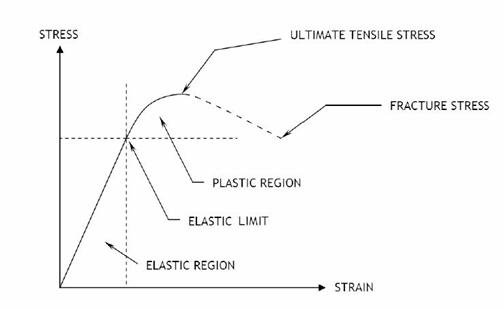
A stress-strain curve graphically shows the relationship between the stress and strain of a material under load. Figure 8 shows the stress-strain curve of a common metallic building material. In the elastic region, the material will regain its original shape once the stress or load is removed. Note that the elastic region in Figure 8 is fairly linear. The slope of this linear portion of the stress-strain curve is the elastic modulus, as defined above.
The elastic limit for a material is the maximum strain it can sustain before it becomes permanently deformed (i.e. if the stress is decreased, the object no longer returns to its original size and shape). In the plastic region, the material loses its elasticity and is permanently deformed. A linear approximation with the elastic modulus is no longer accurate. The ultimate tensile strength is the maximum stress a material can undergo. The fracture stress is the point at which the material breaks. Fracture stress is lower than the ultimate tensile strength of a material as by the time a material reaches that level of stress, it has already begun to rip apart. Thus, the cross-sectional area is constantly decreasing until the material finally breaks.
In addition to these intrinsic materials factors, the behavior of materials as they age and are used in service must be considered in boom design. These factors do not relate directly to the boom design in this lab, but they must be considered when deciding what material to use for an actual design. The loss of desirable properties through use, called fatigue, is important. Non-static loads, repeated loading and unloading, or loads that include vibrations or oscillations will eventually lead to failure in service. Special care must be taken with live loads and situations where small motions may be magnified by design features.
There are many factors to consider in any design project. When designing and constructing the boom for this competition, remember to consider the materials being used and what might cause those materials to fail under a load.
Simulations
An extremely important tool in an engineer’s skillset is the use of simulation tools. Many times, complex designs require quick analysis that cannot be done by calculation or prototyping, so simulation comes in handy and as it saves both time and money. Specifically, Finite Element Analysis (FEA) is a process that a computer software undergoes to simulate a desired scenario. The software calculates mathematical formulas at hundreds to thousands of points on a design, referred to as a mesh, and computes them simultaneously to get a complete look at what would happen. This simulation only works for isotropic materials, meaning that the materials properties (tensile strengths, modulus, etc.) are the same for all sides of the material. This may not be true for certain materials, and an engineer must take this into account. While members of the group are designing and building a boom, others will simulate a basic design in order to understand the effect of the forced displacement, and use that information to improve the initial design.
Fusion 360
A brief digest of the tools and functions of the Fusion 360 Design workspace is presented below. This digest is specific to this virtual lab and many of the CAD functions can be performed differently in other situations.
- The Orbit tool allows rotating the current view around a pivot point in three dimensions. This can also be done by grabbing the orthographic cube in the top right corner and rotating it. To make the view normal to a face, edge, or corner, click the respective part of the orthographic cube.
- The Zoom tool allows for the magnifying or minimizing of an object.
- If the component is lost in the view, either use the Pan tool to move the current view in 2D until it is found, or click Zoom Window > Fit. These tools will help navigate the workspace while putting together the boom.
Moving Components
- Once a component is placed into the workspace, Fusion 360 will remember the component in that space. To move it again, use the Move/Copy tool after right clicking the component (Figure 10).
- Once the component is moved to the desired position, use the Capture Position tool to set the component in that place (Position > Capture Position). If it is ever moved unintentionally, use the Revert button (Position > Revert) to move the component back to its original position. These tools will only show up when the model is an unsaved position (Figure 11).
Deleting Components
- Deleting parts requires an extra step. Clicking on an object automatically selects the face of a body and not the whole body, and Fusion 360 will not be able to delete a face. To get past this, in the toolbar go to Select > Selection Priority > Select Body Priority (Figure 12).
- A part can only be deleted by selecting its body. Make sure to use the same steps to change the selection priority back to face, or to edge/component if necessary. Another way to delete is to right click on the component in the Browser tab and click Delete.
Aligning Components
- The Align tool is found under the Modify tab of the toolbar. This is useful when attempting to place cylinders in a position defined by an opening. Simply select the outside face of the cylinder and the inside face of the hollow cylinder to align the two parts. Make sure to check the Capture Position Box or use the Capture Position tool to save this setup of the model (Figure 13).
Changing Boom Length
- To cut a part of the boom, first open the boom file by double clicking on it from the Data Panel.
- Click on the circular face of the boom. In the toolbar, go to Modify > Press Pull. Use the blue arrow in the current view to change the length of the boom, or type in the desired change in Distance.
- Use Save as to make a new component with a different name. Only the total length supplied by the materials provided can be used (do not increase the length of the full dowels or skewers).
Competition Rules
The competition rules must be followed at all times during the competition. Violation of any of these rules will result in the disqualification of the design.
- The boom is to be secured (i.e. anchored) to the white plastic anchorage
- The boom must extend at least 1.5 m horizontally from the front edge of the anchorage
- The boom may not touch anything but the anchorage
- The basic weight ratio (3) for the competition uses the reaction force in Newtons divided by the boom mass in kilograms.
(3)
The winning design will be determined by the weighted design ratio (4), which uses the weight ratio and boom length in meters divided by 1.5 m.
(4)
Design Considerations
- Which aspects of the competition ratio are most advantageous?
- How can the boom be built and/or reinforced to prevent as much deflection as possible?
Materials and Equipment
The following are the materials that can be used in Fusion 360:
- 2 thick dowels (1.1 cm × 122 cm)
- 2 thin dowels (0.8 cm × 122 cm)
- 6 bamboo skewers (30.5 cm)
- Unlimited dowel connectors
- Boom anchor
Procedure
Build a boom using Fusion 360, simulate it deflecting 20 cm, and record the reaction force. The boom will be entered into a competition against other boom designs in the section.
1. Design the Boom
- Before starting on Fusion 360, sketch the design of the boom and plan its structure. Consider how it will react to a load placed on its end. Determine which materials would be best to use. Do not simply copy the sample boom, be creative.
Note: Fusion 360, like all software, can take time to learn for new users. Reach out to a TA for any help and clarification needed. Some useful tools and functions are given in the Overview section but learn Fusion 360’s panels and functions beforehand.
2. Importing Parts
- The parts for the boom can be found in a ZIP folder here. The latest version of Fusion 360 must be downloaded for the parts to appear properly.
- Unzip the parts to a space on the computer.
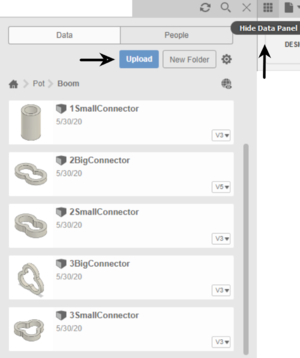
- In Fusion 360, open the Data Panel (icon with 9 boxes at the top left) and click Upload. Select the unzipped part files to upload them to Fusion 360’s cloud memory (Figure 14). Fusion 360 can only import files uploaded to its cloud.
3. Model the Boom
- Ensure that the Design workspace is open in Fusion 360. This is indicated at the top left.
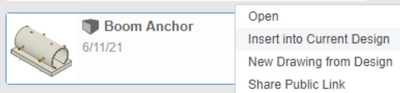
- The part files can be inserted into a new Fusion 360 file by simply dragging and dropping them from the Data Panel into the space. Alternatively, right click the components and select Insert into Current Design (Figure 15). Save the blank file before assembling the boom by going to File > Save as.
- The first part that is inserted into Fusion 360 acts as the base for the entire model. The boom anchor should be inserted first as the boom should be designed around it.
- Import the other parts based on the design that was sketched. Connect all the parts using the Align tool to complete the model. Use the tips from the Fusion 360 section in the Overview.
- Take time to get comfortable with moving each part around. Keep in mind that Fusion 360 is a 3D workspace and depth is not shown on a 2D screen, so use the orthographic cube at the top right of the workspace to change the view and ensure the components fit together.
- A short video is provided for reference here.
4. Evaluate the Boom
Mass of the Boom
- After completing the model of the boom in Fusion 360, switch the workspace from Design to Simulation at the top left of the screen. In the New Study dialog that appears, select Static Stress > Create Study.
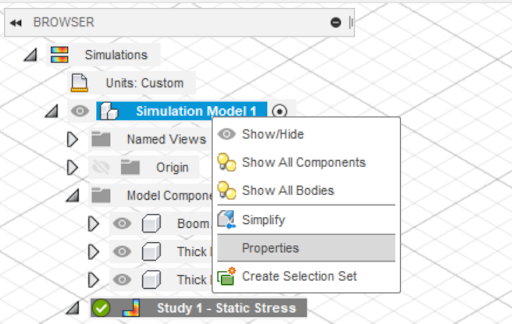
- Go to the Browser on the left-hand side of the Simulation workspace. Right click 'Simulation Model 1' and select Properties (Figure 16).
- In the Properties dialog that appears, record the mass of the body.
Length of the Boom
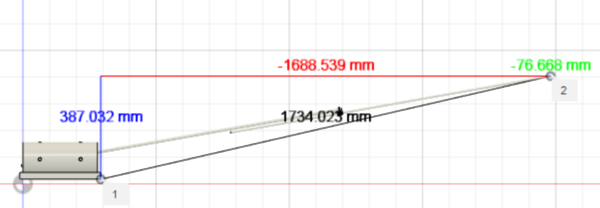
- In the toolbar, go to Inspect > Measure.
- In a side view of the boom, select a point at the front of the anchor and then another point at the tip of the boom.
- In the Measure dialog, check the XYZ Delta box.
- From the Measure dialog, record the length in meters in your Lab Notes.
5. Simulate the Boom
- Make sure that you are in the Simulation workspace. The Simulation toolbar in Fusion 360 lays out the steps from left to right that must be taken to fully run a simulation (Figure 18).
- To study and change the type of material, in the Simulation toolbar go to Materials > Study Materials.
- In the Study Materials dialog, ensure all the parts have ABS plastic as their material, including the dowels (Figure 19). Click OK. Note: ABS is the most commonly used plastic and an isotropic material, meaning its material properties are the same in all directions. This is why running simulations on wood, which is orthotropic (directional) based on grain, is mathematically more difficult.
- To ensure that the boom is not floating in free space and that the load will be properly applied to the boom, a fixed face must be added. In the Simulation toolbar, go to Constraints > Structural Constraints.
- Select the bottom face of the anchor as the Targets. Ensure the Type of constraint is Fixed. The Structural Constraints dialog should look like Figure 20. Click OK.
- The loads on the boom will be simulated using a second constraint. This will force the tip of the boom downwards 20 cm and the reaction force upward will show the simulated downward force.
- In the Simulation toolbar, go to Constraints > Structural Constraints once again.
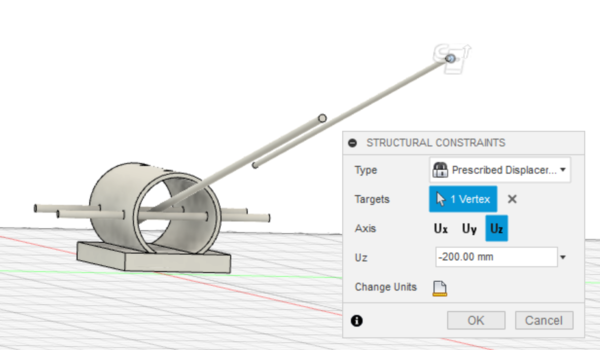
- Change the Type of constraint to Prescribed Displacement. For the Targets, select a point on the edge of the boom.
- Set the displacement to 20 cm downwards (the value should be negative to signify a downward force) (Figure 21). Check the units before entering the value. The downward axis may be different than that of Figure 21 if the boom is oriented differently. Check the axis and then decide the direction of deflection. Click OK.
- Simulation contacts describe the interaction between parts in an assembly. The contacts will be set automatically and manually checked. This is usually where most problems with the simulation occur, so ensure the boom parts are connected and those that should not be connected are not connected.
- In the Simulation toolbar, go to Contacts > Automatic Contacts. Enter a tolerance of at least 5 cm. Click Generate.
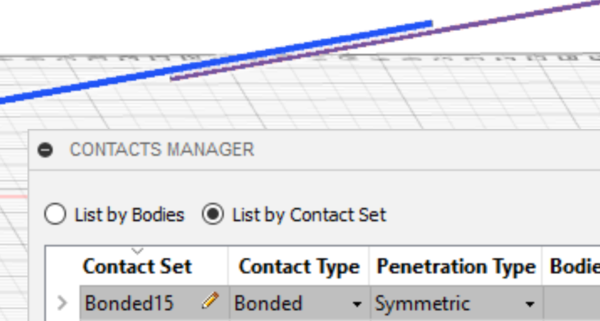
- Go to Contacts > Manage Contacts in the Simulation toolbar to ensure the contacts are correct. Set all contacts to a Contact Type of Bonded. Check to see that each contact is supposed to be a contact. Fusion 360 will highlight the two components that are in contact (Figure 22). Click OK.
- A mesh will now be generated. Go to the Browser tab and right click on Mesh. Click Generate Mesh. The model should appear as a collection of polygonal shapes.
- The results will now be calculated and obtained. In the Browser tab, right click Results > Solve. In the Solve dialog, click Solve 1 Study. Wait for the simulation to complete.
6. Interpret the Results
- After the simulation has been solved, the workspace will show a deflected boom similar to the one shown below in Figure 23.
- The scale on the right displays the Safety Factor, which can range from 0-15. Make sure the minimum safety factor is above 1.
- If the safety factor is below 1 anywhere other than the tip of the boom, the materials have failed. Check for the areas of discrepancy, making sure the contacts and the displacement are set properly, and run the simulation again. If this persists, state that the simulation had a safety factor of less than 1 and the materials failed.
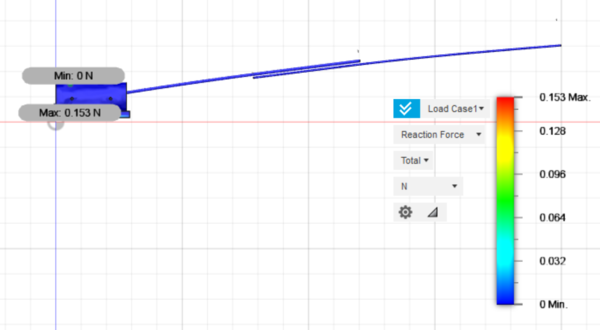
- The boom should be straight and deflect downward relatively evenly. If the boom does not look like the boom shown in Figure 23, increase the tolerance of the contacts by creating another set of Automatic Contacts. Ensure the boom is deflecting downwards and on no other axis, and that the deformation is set on Actual (Results toolbar > Deformation > Actual). Ensure the Reactions are being observed (Results toolbar > Inspect > Reactions). The toolbar should look like Figure 24. The maximum reaction force and point of failure may be at the tip of the boom. This is fine and merely a consequence of the mesh.
Finding the Reaction Force
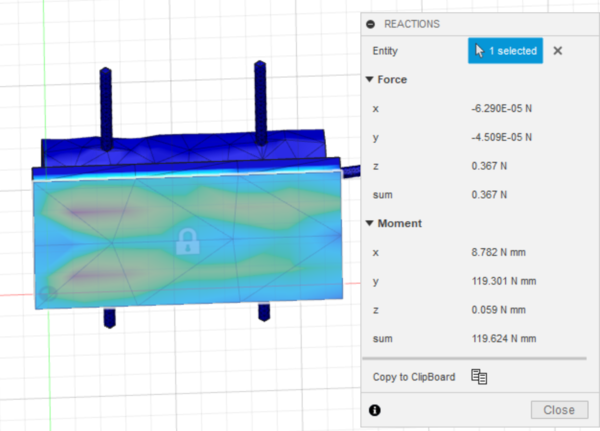
- The reaction force will be determined. In the Results toolbar, go to Inspect > Reactions and click the bottom face of the boom anchor as the Entity. There is a force on the bottom face of the boom anchor that is a resultant of the 20 cm displacement at the end of the boom. This is the reaction force.
- From the Reactions dialog, record the axial force on the same axis that the displacement was directed on (Figure 25). It should be the largest of the three axial forces.
- The reaction force will be used to calculate and record the weight ratio and design ratio of the boom.
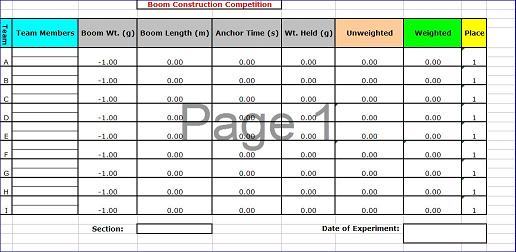
7. Competition
Give the length, mass, and reaction force of the boom design to a Lab TA. The Lab TAs have prepared an Excel file with the section's competition results. It can be accessed in the Lab Documents section of the EG1004 website. This chart must be included in the PowerPoint presentation and in the Data/Observations section of the lab report. All competition labs will include a competition scoresheet for the section that will be referenced to in the assignment. Take a screenshot of the designed boom and send it to the Lab TA. The lab work is now complete. Refer to the Assignment section for the instructions needed to prepare the lab report.
Assignment
Individual Lab Report
Extra Credit OpportunityStudents who perform well on this report have the opportunity to replace a lower score on an earlier lab report with their score on this report. |
Follow the lab report guidelines laid out in the EG1004 Writing Style Guide in the Technical Writing section of the manual. Use the outline below to write this report.
- Describe the rules of the competition. What consequences did the rules have on any design decisions? Use the appropriate equations in your answer.
- What factors were considered in designing the boom? Was any of the background information used? (Hint: Explain the basic concepts behind stress and strain learned)
- What was the basic weight ratio and weighted design ratio for the designed boom?
- Describe how the components chosen functioned in the design, and describe its height/length/shape
- Describe the advantages and disadvantages of the boom design
- Discuss design improvements. How can the design be optimized (i.e. improve the ratio) based on experience?
- Which elements of the boom (e.g. dowels, 3D printed dowel connectors, etc.) were stressed by the load, in what directions, and contributed to the deformation/failure?
- How can simulations be helpful in predicting real world models?
- Does the simulation tell us everything about the system? If not, how can the results of the simulation be manipulated to give an approval of safety for the real life design?
- Include the spreadsheet with every boom's results. Describe the results and talk about other designs in the class
- Describe the process of designing the boom and state the changes seen during this process
- How was your design any different from the other designs?
Remember: Lab notes must be taken. Experimental details are easily forgotten unless written down. Use the lab notes to write the Procedure section of the lab report. One point of extra credit is awarded if the lab notes are attached at the end of the lab report. Keeping careful notes is an essential component of all scientific practice.
Team PowerPoint Presentation
Follow the presentation guidelines laid out in the EG1004 Lab Presentation Format in the Technical Presentations section of the manual. When preparing the presentation, consider the following points.
- How can the boom design be improved?
- Other than the examples given in this lab, what are other examples of booms?
- Which elements of the boom (e.g., wooden dowels, 3D printed dowel connectors, Kevlar string, etc.,) were stressed by the load, in what directions, and contributed to the failure?
References
How Stuff Works website. 2003. SHW Media Network. Retrieved July 28, 2003. http://science.howstuffworks.com/tower-crane3.htm
Jennings, James. 2015. “Up, UP in a Crane: What Life is Like as a Tower Crane Operator.” Philadelphia. Accessed 14 January 2020 from www.phillymag.com
Serway, R., Beichner, R., Physics for Scientists and Engineers with Modern Physics, 5th Edition. Fort Worth, TX: Saunders College Publishing, 2000
| ||||||||





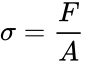
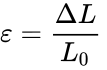
![{\displaystyle Weight\ Ratio={\frac {Reaction\ Force\left[{\text{N}}\right]}{Boom\ Mass\left[{\text{kg}}\right]\times \ 10}}\,}](https://wikimedia.org/api/rest_v1/media/math/render/png/0d11c221af96a92e29c9a88dd078e276b561306d)
![{\displaystyle Design\ Ratio={\frac {Reaction\ Force\left[{\text{N}}\right]}{Boom\ Mass\left[{\text{kg}}\right]\times \ 10}}\times {\frac {Boom\ Length\left[{\text{m}}\right]}{1.5\left[{\text{m}}\right]}}\,}](https://wikimedia.org/api/rest_v1/media/math/render/png/f078bc61acc3a4e4977c5c1f43dacd14d560d151)