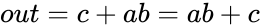|
|
| (3 intermediate revisions by one other user not shown) |
| Line 1: |
Line 1: |
| {{SLDP: RFP|Nuclear Regulatory Commission (NRC)}} | | {{SLDP:|Nuclear Regulatory Commission (NRC)}} |
| | |
|
| |
|
|
| |
|
| = Introduction and Overview = | | = Introduction and Overview = |
| | With the recent spike in water and air based pollution illness is on the rise. The center of disease control has hired you to work on the newly funded project testing different types of nano robotics on the ill and dying. Your patient, Jessy, has volunteered to go through this trial and has entrusted their well being to you and your ability to work with these nano robotics. Jessy is ravaged with disease please program a nano robot to travel through their body, diagnose their diseases and cure them or they'll die. |
|
| |
|
|
| |
|
| == Prerequisite == | | == Prerequisite == |
| If you have not already done the [[Digital Logic]] Lab, you will probably find the rest of this document confusing. If you have not already done this lab, stop now and read the [[Digital Logic#Overview|Overview]] and [[Digital Logic#Sample Problem|Sample Problem]] sections of the lab.
| |
|
| |
|
| It is strongly advised that you familiarize yourself with the following digital logic topics before attempting to tackle the problem that is set before you in this project. In addition to familiarizing yourself with these topics, please make sure that you are also able to answer the questions that are very closely related to the task at hand.
| |
| # Boolean Algebra
| |
| ## What are the only 2 possible values of a variable in Boolean algebra?
| |
| ## What are the 3 most commonly used logical Boolean operators and what do their corresponding truth tables look like?
| |
| ## How do the aforementioned operators appear in a sample Boolean equation?
| |
| # Truth Tables
| |
| ## How does the amount of input variables affect the size of a given truth table?
| |
| ## What is the procedure for setting up 2, 3, 4, and 5 variable truth tables?
| |
| # Boolean Equations
| |
| ## How to derive a Boolean equation from a 2, 3, 4, and 5 variable truth table?
| |
| ## What are some of the techniques that you can use in order to simplify a Boolean equation?
| |
| # Karnaugh Maps
| |
| ## What is the procedure for setting up 2, 3, and 4 variable Karnaugh maps?
| |
| ## What is the relationship between the amount of cells in a Karnaugh map and the number of rows in a truth table?
| |
| ## How to properly match up cells in a Karnaugh maps and their corresponding rows in a Truth Table?
| |
| ## What is the procedure for simplifying Boolean Equations using Karnaugh Maps?
| |
| Many if not all of these questions can be answered by reading and performing Experiment 5: Digital Logic, so you are '''STRONGLY''' suggested to get solid background in Digital Logic before continuing with this semester long design project. The answers to these questions are located in [[#Appendix D: Preparation Question Answers|Appendix D]].
| |
|
| |
|
| = Specifications = | | = Specifications = |
| As part of this project, you are required to use digital logic to design Boolean equations that will be used to control the track switches along the right of way. This includes creating truth tables, transforming these truth tables into simplified Boolean equations, and implementing your equations with digital logic, using LabVIEW to control the train track, allowing a locomotive to safely navigate the track from left to right, and back again.
| | Using the virtual or physical model of Jessy depicting the location of the diseases, try to determine what the disease could be based on how the leds are acting in the body and compare that to the disease list found below. |
| | |
| The route the train can take is controlled by track switches arranged into 8 '''''sectors''''', as shown in Figure 1. The sectors are outlined using the dark gray color in the figure underneath. Sectors 1, 4, 7, and 8 are called "X" sectors because the combination of the four track switches make a letter "X", and the train can either travel straight or cross over to another track. Sectors 2, 3, 5, and 6 are called "Y" sectors because the sector consists of a single track switch that looks like the letter "Y", and can choose one of two tracks to merge with one track.
| |
| | |
| [[Image:RTGS2.png|frame|right|Figure 1b: Track Layout Key]]
| |
| [[Image:RTGS1.jpg|frame|none|Figure 1a: Track Layout]]
| |
| | |
| Your logic design will throw the track switches to allow a train to travel from any track at Terminal Station L (i.e., L1, L2, or L3) to any track at Terminal Station R (i.e., R1, R2, or R3), reverse direction, and travel back from Terminal Station R back to Terminal Station L. The train can leave from any track of the Terminal Station L, and can arrive on any track of Terminal Station R. Similarly, on the return trip, the train can arrive on any track of Terminal Station L.
| |
| | |
| There are two configurations (modes) that the train must abide by:
| |
| * Normal Mode
| |
| * Reverse Running Mode
| |
| | |
| In '''Normal Mode''', defined by MTA New York City Transit:
| |
| * '''Left-To-Right Travel'''
| |
| ** Only the Sectors 2, 4, 6 and 8 tracks are allowed to be switched on
| |
| ** The other 4 sectors are disabled and '''''MUST''''' remain in their default ('''STRAIGHT''') position throughout the test run
| |
| ** Train must remain on the '''BOTTOM''' half of the track
| |
| ** If starting from L1, the No Path condition automatically exists
| |
| * '''Right-To-Left Travel'''
| |
| ** Only Sectors 7, 5, 3, and 1 are allowed to be switched on
| |
| ** The other 4 sectors are disabled and '''''MUST''''' remain in the default ('''STRAIGHT''') position throughout the test run
| |
| ** Train '''MUST''' remain on the '''TOP''' half of the track
| |
| ** If train starts at R3, the No Path condition automatically exists
| |
| In summary, while operating in ''Normal Mode'' the train must "keep to the right", like cars on a highway. The train is allowed to pass disabled sectors but you are not allowed to apply signals in order to switch them. This makes your job as a logic designer very simple as it eliminates approximately half of the obstacles for each direction of travel.
| |
|
| |
|
| In Reverse Running Mode, as defined by the Northeast Operating Rules Advisory Committee Rule 261:
| | There are two programs available to work with the nano robot, python and a digital program. |
| * All the tracks can be used to travel in either direction
| |
| * Your logic is allowed to and should utilize all available switches and light sensors in order to try and guide the train from one side of the track to the next
| |
|
| |
|
| '''''You are asked to take careful note and know the difference between Normal and Reverse modes as this knowledge will help you in the crucial process of designing your LabVIEW Virtual Instrument. It will also impact several key decisions for this project down the line. (Following this, Virtual Instrument will be referred to as VI in this document.)'''''
| |
|
| |
| <!-- For ''Normal Mode'', the train leaves Terminal Station L, and crosses Sector 1, if necessary, to get to Sector 2. At Sector 2, you have a choice of using the inner or outer track. Since the optimal path between two points is a straight line, its ideal path would be the inside tracks of Sectors 2, 4, and Sector 6, crossing Sector 8, if necessary, to arrive on the proper track at Terminal Station R. For the return trip, the train would cross Sector 8, if necessary, to get to Sector 7. Its ideal path would be the inside tracks of Sectors 7, 5, and 3, crossing Sector 1, if necessary, to arrive on the proper track at Terminal Station L. -->
| |
|
| |
|
| == Task == | | == Task == |
| Your train will not be the only train present on the tracks during testing. As part of the specifications, there will be 12 possible locations for other trains to be on the tracks creating obstructions for the traveling train. The locations at which these trains can be present are indicated with [[Image:RTGS3.png]] and are marked with a letter A – L on the following diagram. Your Boolean equations and LabVIEW programs must compensate for this, and allow your train to get through based on which operating mode is set.
| |
|
| |
| It is possible that the obstacles present on the tracks do not allow for the train to get through to the other side, this case is known as "No Path." Your VI must have an indicator light to show the operator that there are no possible paths that can be taken in order to avoid the obstacles placed on the tracks. "No Path" conditions will depend heavily on the starting position of the train (L1, L2, L3 or R1, R2, R3), direction of travel (Left-To-Right or Right-To-Left) as well as the mode of operation (Normal or Reverse). Your VI must take into account all of these variables and be able to deliver the correct logic in order to verify whether a "No Path" condition exists on the tracks or not.
| |
|
| |
| [[Image:RTGS4.jpg|frame|none|Figure 2: Possible Locations for Other Trains]]
| |
|
| |
| '''''Your task is to design a digital logic system that will allow the train to travel from one end of the track layout to the other, and to return to the starting point using the designated departure and arrival tracks. During testing, your TA will choose different locations, A through L, to block different sections of track. Your logic will then throw the train switches (as described below) to allow the locomotive to travel from Terminal Station L to Terminal Station R, where the locomotive will stop. The TA will change the locations of the blocked track sections, and your logic will throw the switches for the return trip.'''''
| |
|
| |
| The EG staff has already done much of the work for you, providing Virtual Instruments (VIs) that will tell you which of the locations in Figure 2 are blocked, and accepting outputs from your VI as described below to actually throw the track switches. Design a LabVIEW VI which contains a digital logic circuit that accepts the following inputs:
| |
| * The status of each of the 12 locations, i.e., whether they are occupied or not. This information will come from a VI provided by the EG staff.
| |
| * A switch included in LabVIEW that indicates the direction of the train's travel, i.e., from left to right or right to left.
| |
| *A switch included in LabVIEW that indicates whether the train's travel will be via ''Normal Mode'' or ''Reverse Running Mode''.
| |
| * A selection box included in LabVIEW that will indicate on which the train will begin its journey (Top, Middle, Bottom for L1/R1, L2/R2, and L3/R3 respectively. Please consult [[#Appendix C|Appendix C]] for a description and a walkthrough on how to create, configure, and use a selection box that you will need for Benchmark Assessment A.
| |
|
| |
|
| Your digital logic must provide the following outputs:
| |
| * If one or more paths is available, supply the digital logic outputs for the settings of the track switches for each of the eight sectors to the VI provided by the EG staff. This VI will throw the switches according to your specification, allowing the train to travel from one Terminal Station to the other.
| |
| * A red light included in LabVIEW on the ''Front Panel'' that illuminates if there is no path available.
| |
|
| |
| After your VI has set the switches, your TA will drive the train from the Terminal Station L to Terminal Station R, and change the locations of the blocked tracks. After your VI sets the switches for the return trip, your TA will drive the locomotive back to the Terminal Station L. The TA will perform this procedure several times to ensure that you logic solution is indeed correct.
| |
|
| |
| {{SLDP: Microsoft Project}}
| |
|
| |
|
| == Cost Estimate == | | == Cost Estimate == |
| You will need to create a cost estimate using quotes from a reputable vendor. Examples are [http://www.digikey.com Digikey], [http://www.newark.com Newark Electronics/Newark In One], and [http://www.onsemi.com On Semiconductor]. You are not limited to these vendors. This cost estimate includes prices for TTL Logic Chips for the various logic gates you use in your LabVIEW VI. When doing your cost estimate, be sure to include specification sheets from the vendors for all of the chips that you may use. | | You will need to create a cost estimate using quotes from a reputable vendors. You are not limited to these vendors. When doing your cost estimate, be sure to include specification sheets from the vendors. |
|
| |
|
| Create a cost estimate on a Microsoft Excel spreadsheet. The cost estimate should include the following: | | Create a cost estimate on a Microsoft Excel spreadsheet. The cost estimate should include the following: |
| Line 115: |
Line 48: |
| * Be sure to include any special features and benefits of your design. | | * Be sure to include any special features and benefits of your design. |
|
| |
|
| === Introduction to RTGS Digital Logic === | | === Introduction to NRC Programming === |
| ''Refer to [[#Appendix D: Boolean Logic|Appendix D: Boolean Logic]] for more details''
| |
| | |
| When the train leaves the left terminal from middle position, the Sector 1 switch is in place to allow the train to travel outbound toward Sector 3 or straight toward Blocking Signal B. When the train leaves the terminal from the top position, the Sector 1 switch is in place to allow the train to travel straight toward Sector 3 or cross toward Blocking Signal B. When the train leaves the terminal from the bottom position, Sector 2 allows the train to continue straight or cross toward Blocking Signal C. You will be creating a Boolean Equation to determine which sector to use, based on which locations on the tracks are blocked. '''''For this Milestone, your train will operate in REVERSE MODE, meaning it can take any possible path in order to avoid a collision.''''' In the following milestones as well as your semester long design project you will incorporate the logic you create for Milestone 1 into your project.
| |
| | |
| For this milestone, we will create a plan for the train to leave Terminal Station L. This includes having the logic necessary for the train to be able to successfully navigate the first three (3) sectors, while ignoring the first blocking signal (Blocking Signal A). '''''<span style="color: red">You will NOT be physically programming in LabVIEW for this Milestone, but instead developing your plans on paper using Truth Tables, Karnaugh Maps and Boolean Equations</span>'''''. If you do not yet feel comfortable with utilizing these tools, please go back to the [[Digital Logic]] lab or seek out reliable source (Written / Internet) in order to learn how to properly utilize them. You will be creating a Boolean equation to determine which sector to use, based on which locations on the tracks are blocked. '''''For this portion of the project, your train will operate in REVERSE MODE, meaning it can take any possible path in order to avoid a collision'''''. In the following milestones as well as your semester long design project you will use the experience gained to help you complete the tasks ahead.
| |
| | |
| [[Image:RTGS5.jpg|frame|none|Figure 3: Sample Terminal with switch]]
| |
|
| |
|
| Here are the Boolean variables you will need to create the equation:
| |
| # Let T represent the track that the train is on at the terminal. T can take on one of three values (Top, Middle, Bottom), which means that 3 separate truth tables have to be generated, each for every starting position. Furthermore, since there are a total of 3 sectors for this Milestone, you will need to generate a truth table for each Sector as well. Finally, there is also NO PATH logic for each sector, this makes a total count of Truth Tables for this milestone equal to 12. (For example: Starting on top position and sector 1 logic, starting on middle position and sector 3 logic.)
| |
| # Let A, B, C, and D represent a train blocking the respective portion of the track.
| |
| # If A, B, C, or D = 0, the corresponding track is free of obstacles. If A, B, C, or D = 1, the corresponding track is blocked.
| |
| # Let S represent the status of the sector. For simplicity, there are only two values. When S=0, any train passing over the switch will stay on course and go straight. When S=1, any train passing over the switch will be diverted to the other track, in other words cross the track.
| |
| # Let N represent whether or not the train can proceed through the switch through the specified operating sections. This condition is also known as the "NO PATH" condition. When N=1, the right of way is blocked, and the train cannot proceed to the end of the section by using any possible combination of paths. When N=0, the track is clear, and the train can proceed through the switch by taking some possible combination of paths.
| |
|
| |
| [[Image:RTGS6.jpg|frame|none|Figure 4: Represents the three sectors that need to be completed for Milestone 1]]
| |
|
| |
| Create a truth table for each starting position for each sector showing every possible outcome. (See example below. Keep in mind that the example below COMBINES 4 truth tables into 1, since each of those 4 truth tables contain the same input variables) Once you create 12 truth tables, proceed to create Boolean equations based upon your truth tables. Create Karnaugh-Maps (K-Maps) and use them to simplify the Boolean equations (if possible). See the [[Digital Logic]] lab in this manual for further assistance. Remember, once these steps are complete you will have three equations (one for each starting position L1, L2, and L3) for sectors S<sub>1</sub>, S<sub>2</sub>, S<sub>3</sub> and three equations (one for each starting location) for N (No Path).
| |
|
| |
| {| class="wikitable" style="float: right; text-align: center;"
| |
| |+ style="caption-side: bottom; font-weight: normal; text-align: left;"|Figure 5b: Along with your table make sure to include a legend (key).
| |
| !colspan="3"|Legend
| |
| |-
| |
| !rowspan="2"|Blocking Signals (B, C, D, E)
| |
| |0||Free of obstacles
| |
| |-
| |
| |1||Blocked
| |
| |-
| |
| !rowspan="2"|Switch Sectors (S<sub>1</sub>, S<sub>2</sub>, S<sub>3</sub>)
| |
| |0||Straight
| |
| |-
| |
| |1||Cross
| |
| |-
| |
| !rowspan="2"|No Path (N)
| |
| |0||Train can proceed
| |
| |-
| |
| |1||Train CANNOT proceed
| |
| |-
| |
| |}
| |
| [[Image:RTGS7.png|frame|none|Figure 5a: Example truth table, this truth table incorporates 4 sets of logic, S<sub>1</sub>, S<sub>2</sub>, S<sub>3</sub> and N. Your truth tables can take a similar format or can be split up into separate truth tables.]]
| |
|
| |
|
| == Benchmark Assessment A == | | == Benchmark Assessment A == |
| In Milestone 1, we created a plan for the train to leave Terminal Station L, pass through Sectors 1, 2, 3 and stop. For Benchmark Assessment A, we will be creating another, more complex plan. This time, you will need to create necessary Boolean logic relationships and equations for the train to travel through Sectors 4, 5, 6 making use of Blocking Signals A, B, C, D, E, F, G, H and translate that information into a LabVIEW VI. Furthermore, you will need to accomplish this task for both modes of operation, Normal as well as Reverse. Remember, you only considered the Reverse mode for Milestone 1. While traveling from left to right under Normal mode of travel, the only sectors that are allowed to be switched are 2, 4, 6, and 8 while sectors 1, 3, 5, and 7 '''''<span style="color: red">MUST BE LEFT</span>''''' in their default position (Straight). Since Sector 8 is not in the scope of this benchmark, you do not need to worry about logic for Sector 8. Your solution may incorporate the logic you developed for Milestone 1. If you choose to use the equations you have already written for the first milestone, you will have to account for the fact that there are now more input variables, some of which may have an effect on the logic for a particular switch. Revising your logic equations instead of creating completely new ones will greatly simplify your problem as you won’t have to repeat the work you have already done. '''''Keep in mind that for this and upcoming benchmarks as well as the final project submission, the number of variables in some cases may make the traditional way of solving digital logic problems (truth table, Karnaugh map) not feasible (If you are dealing with more than five variables), in this case you should manually find all cases in which a particular track sector should switch.''''' In short the following equations need to be written:
| |
|
| |
|
| : '''Direction of Travel''': Left-To-Right
| |
| : '''Travel Mode''': '''<span style="color: red">Normal</span>'''
| |
| : '''Starting Positions''': L1, L2, L3
| |
| : '''Sectors''': 2, 4, and 6 (''Keep in mind that since S<sub>1</sub> is disabled in Normal mode, the L1 starting position creates a "No Path" condition regardless of any track conditions.'')
| |
| : '''Total Number of Boolean Equations''': (L2 S<sub>2</sub>, L2 S<sub>4</sub>, L2 S<sub>6</sub>, L3 S<sub>2</sub>, L3 S<sub>4</sub>, L3 S<sub>6</sub>, L2 No Path, L3 No Path) &mdashl; 8 equations
| |
|
| |
|
| : '''Direction of Travel''': Left-To-Right
| |
| : '''Travel Mode''': '''<span style="color: red">Reverse</span>'''
| |
| : '''Starting Positions''': L1, L2, L3
| |
| : '''Sectors''': 1, 2, 3, 4, 5, and 6
| |
| : '''Total Number of Boolean Equations''': ( L1 S<sub>1</sub>, L1 S<sub>2</sub>, L1 S<sub>3</sub>, L1 S<sub>4</sub>, L1 S<sub>5</sub>, L1 S<sub>6</sub>, L2 S<sub>1</sub>, L2 S<sub>2</sub>, L2 S<sub>3</sub>, L2 S<sub>4</sub>, L2 S<sub>5</sub>, L2 S<sub>6</sub>, L3 S<sub>1</sub>, L3 S<sub>2</sub>, L3 S<sub>3</sub>, L3 S<sub>4</sub>, L3 S<sub>5</sub>, L3 S<sub>6</sub>, L1 No Path, L2 No Path, L3 No Path) &,dash; 21 Equations
| |
|
| |
| Here are the Boolean variables you will need to create the equation. Many of the conventions have stayed the same from Milestone 1 and will stay the same until completion of the project:
| |
| # Let T represent the track that the train is on at the terminal. As before T can take on 3 possible values, Top, Middle, and Bottom.
| |
| # Let C represent a train blocking input C.
| |
| # Let D represent a train blocking input D.
| |
| # Let E represent a train blocking input E.
| |
| # Let F represent a train blocking input F.
| |
| # Let G represent a train blocking input G.
| |
| # Let H represent a train blocking input H.
| |
| # If C, D, E, F, G, or H = 0, the corresponding track is free of obstacles. If C, D, E, F, G, or H = 1, the corresponding track is blocked.
| |
| # Let S<sub>1</sub> represent the status of the switch at Sector 1. Let S<sub>2</sub> represent the status of the switch at Sector 2. Let S<sub>3</sub> represent the status of the switch at Sector 3. When S<sub>1</sub>, S<sub>2</sub>, or S<sub>3</sub> = 0, the train goes straight through. When S<sub>1</sub>, S<sub>2</sub>, or S<sub>3</sub> = 1, the train crosses over on to the other track.
| |
| # Let N be the "No Path" condition and represent whether or not you can proceed through the switches to one track or another. When N=0, the path is clear, and the train can proceed. When N=1, all paths are blocked, and the train cannot proceed through the track by utilizing any combination of switched tracks.
| |
|
| |
| On the front panel, you will need:
| |
| * 9 Boolean controls, one for each input (A, B, C, D, E, F, G and H), and one to control whether the train is operating in Normal or Reverse mode.
| |
| * You will also need a selector switch that will facilitate the selection of the starting track of the train. (Top, Middle, or Bottom)
| |
| * 7 Boolean indicators, one for each sector (S1, S2, S3, S4, S5, and S6), and one indicating No Path (N).
| |
|
| |
| On the back panel, it is up to you how you will program the VI. '''''<span style="color: red">You are strongly encouraged to use case structures. The problem was set up and broken down so that it would be easier done through the case of case structures.</span>'''''
| |
|
| |
| Please refer to [[#Appendix B|Appendix B]] further down the page for information on how to interface your VI with the Benchmark Assessment A VI before reading on. It is extremely important that this step be performed before you are ready to complete Benchmark Assessment A. Through the use of the 28-node pattern your solution VI will be able to communicate with our tester VI, so make sure to read the instructions on how to configure your VI correctly. You will continue to use the same 28-node pattern to commission your VI once you are ready, so once you have properly configured your 28-node pattern please do not change the ordering of the nodes or clear the node assignments.
| |
|
| |
| Your VI will interface with the RTGS test track by using a custom VI provided by EG. It is located at
| |
|
| |
|
| '''<span style="color: red">C:\SLDP Railroad Train Guidance System\Benchmark Assessment A.vi</span>''' | | '''<span style="color: red">C:\SLDP Railroad Train Guidance System\Benchmark Assessment A.vi</span>''' |
| Line 200: |
Line 60: |
|
| |
|
| == Milestone 2 == | | == Milestone 2 == |
| Update the VI to incorporate the current logic design. Using a screenshot tool, prepare views of the virtual instrument (VI) used to interface with the RTGS test track. Complete the latest MS Project plan reflecting any schedule changes. Finally, calculate a revised cost estimate.
| |
|
| |
|
| '''''Look Ahead''': What tasks are planned between now and Milestone 3?'' | | '''''Look Ahead''': What tasks are planned between now and Milestone 3?'' |
| Line 213: |
Line 72: |
| ** Mission statement | | ** Mission statement |
| ** Samples of logic design | | ** Samples of logic design |
| *** Truth tables
| | |
| *** Karnaugh maps
| |
| *** Boolean equations
| |
| *** VI interface (front and back panels)
| |
| ** Cost estimate (previous and current). What changes were made?
| |
| ** MS Project schedule (previous and current). What changes were made?
| |
| ** Progress update: current state of the project (time, budget, etc.)
| |
|
| |
|
| == Benchmark Assessment B == | | == Benchmark Assessment B == |
| Prepare a VI that will use your Boolean equations to show how the track switches will be set. This includes the entire track utilizing all of the eight sectors, both modes of operation (Normal and Reverse), and at least one direction of travel (Left to Right and Right to Left). This means that at this point your logic and your LabVIEW VI can successfully guide the train from Left-to-Right or Right-to-Left (Depending on the direction you have completed) in either modes of operation. Use Boolean switches in the LabVIEW front panel to indicate which track locations are obstructed. Use lights on the front panel to indicate which switches are set to divert trains traveling over them. Refer to the Train Electrical Specifications for more information. Refer to [[#Appendix B|Appendix B]] for more information on how to interface your VI with the Commissioning VI.
| | |
|
| |
|
| Your VI will interface with the RTGS test track by using a custom VI provided by EG. It is located at | | Your VI will interface with the RTGS test track by using a custom VI provided by EG. It is located at |
| Line 233: |
Line 86: |
|
| |
|
| == Milestone 3 == | | == Milestone 3 == |
| Update the VI to incorporate the current logic design. Using a screenshot tool, prepare views of the virtual instrument (VI) used to interface with the RTGS test track. Complete the latest MS Project plan reflecting any schedule changes. Finally, calculate a revised cost estimate.
| | |
|
| |
|
| '''''Look ahead''': What tasks are planned between now and the completion of the project?'' | | '''''Look ahead''': What tasks are planned between now and the completion of the project?'' |
| Line 255: |
Line 108: |
|
| |
|
| = Commissioning = | | = Commissioning = |
| Refer to the syllabus for the commissioning deadline. There are penalties for not completing on time. Refer to the EG1003 Grading Policy for more information. | | Refer to the syllabus for the commissioning deadline. There are penalties for not completing on time. Refer to the EG1004 Grading Policy for more information. |
|
| |
|
| Load your VI into the PC connected to the train layout, and interface it with the Commissioning Test VI. The Commissioning Test VI can be located at | | Load your VI into the PC connected to the train layout, and interface it with the Commissioning Test VI. The Commissioning Test VI can be located at |
| Line 261: |
Line 114: |
| '''<span style="color: red">C:\SLDP Railroad Train Guidance System\Commissioning Test.vi</span>''' | | '''<span style="color: red">C:\SLDP Railroad Train Guidance System\Commissioning Test.vi</span>''' |
|
| |
|
| on the PC connected to the train layout. Your TA will then place train cars in various locations, and position the locomotive on a track at Terminal Station L. The TA will first test your program using Normal Mode. Set the Boolean switches on your LabVIEW front panel so your VI has this information. When the TA is finished, your VI should read the Boolean switches and locations of the train cars via the VI provided by the EG staff, calculate the proper track switch positions, and output the results to the Commissioning Test VI. This VI will set the track switches according to your specifications. The TA will verify that the path you have established will work. Once your VI establishes a successful path, the TA will drive the locomotive from left to right. After the locomotive arrives on the proper track at Terminal Station R, the TA will rearrange the cars blocking paths for the return to Terminal Station L. Set the Boolean switches on your LabVIEW front panel to indicate this information. Your logic should read the blockage information from the VI provided by the EG staff and set the track switches to the proper position. The TA will verify that you've established a good path, and will drive the locomotive back to the Terminal Station L, arriving on the proper track.
| |
|
| |
|
| After you have tested your VI with normal running, the TA will then test your VI in Reverse Running Mode. The procedure will be the same as the Normal Mode, with the exception of Reverse Running.
| |
|
| |
|
| Finally, your TA will test your VI such that it indicates no path correctly. If your VI completes all tests successfully, you will be commissioned. | | Finally, your TA will test your VI such that it indicates no path correctly. If your VI completes all tests successfully, you will be commissioned. |
| Line 295: |
Line 146: |
| {{SLDP: Late Delivery}} | | {{SLDP: Late Delivery}} |
|
| |
|
| = Appendix A: Train Electrical Specifications = | | = Appendix A: Specifications = |
|
| |
|
| == Output control of the track ==
| |
|
| |
|
| [[Image:RTGS1.jpg|frame|none|Figure 1: Layout of the eight sectors on the train track]]
| | = Appendix B: = |
|
| |
|
| Each part of the track is separated into different sectors. The sectors can be classified into two types, X and Y (refer to the diagram). Sectors 1, 3, 5, and 7 are X type and Sectors 2, 4, 6, and 8 are Y type.
| |
|
| |
|
| There is a Sub-VI that will be provided that will cause the tracks to move depending upon which data is sent to the VI. Only include this Sub-VI in your their logic VI. The Sub-VI has eight inputs which are Boolean named, Sector 1 through Sector 8.
| |
|
| |
| For the X type sectors, a Boolean value of ''True'' will cause the tracks to be oriented for the train to cross. A Boolean Value of ''False'' will cause tracks to be oriented for the train to go straight.
| |
|
| |
| For the Y type sectors, a Boolean value of ''True'' will cause the tracks to be oriented for the train to be diverted to the diagonal track. A Boolean value of ''False'' will cause the tracks to be oriented for the train to travel on the straight track.
| |
|
| |
| == Input from the track ==
| |
|
| |
| [[Image:RTGS4.jpg|frame|none|Figure 2: Layout of the twelve possible positions of obstacles on the train track]]
| |
|
| |
| There are twelve possible locations for train cars which can be located on positions A to L. A Sub-VI will be provided to you that will have twelve Booleans outputs named Input A through Input L. A ''True'' will represent a train car being present and a ''False'' will represent a car not being present on that position. These outputs will be used as the inputs to your digital logic circuit.
| |
|
| |
| = Appendix B: LabVIEW =
| |
|
| |
| '''Note:''' The following instructions are for your VI that will interface with the Benchmark Assessment A, as well as the Commissioning VI.
| |
|
| |
| On the front panel, there must be 12 Boolean switches to represent the 12 inputs of the train, a menu ring to indicate the train's starting position (top, middle bottom), a Boolean switch to indicate whether the train is operating in Normal Mode or Reverse Running Mode, eight Boolean lights to represent each of the eight sectors, and one Boolean light to represent No Path. For Benchmark Assessment A, you will have fewer available Boolean switches and Boolean lights, so only fill in or set the ones that are present on your VI.
| |
|
| |
| [[Image:Train8.jpg|frame|right|Figure 1: Twenty-eight node pattern]]
| |
| * On the front panel of the LabVIEW program, right click on the connector icon on the top right hand corner icon. Choose ''Show Connector''.
| |
| * Right click on the connector icon and select ''Patterns''. Choose the pattern with 28 nodes.
| |
| == Front Panel Object Definitions ==
| |
| When creating your VI, please adhere to the following definitions for the inputs and outputs of your front panel objects. Failure to do so will result in your VI not working as intended when it comes time to commision on the physical track.
| |
| {| class="wikitable" style="text-align: center; margin: 1em auto;"
| |
| !
| |
| !True!!False
| |
| |-
| |
| |style="text-align: left"|Blocking Signals A through K
| |
| |blocked||not blocked
| |
| |-
| |
| |style="text-align: left"|Direction of Travel
| |
| |right-to-left||left-to-right
| |
| |-
| |
| |style="text-align: left"|Travel Mode
| |
| |Reverse Running Mode||Normal Mode
| |
| |-
| |
| |style="text-align: left"|Sectors 1 through 8
| |
| |cross||straight
| |
| |-
| |
| |style="text-align: left"|No Path
| |
| |no path||path exists
| |
| |}
| |
| <br style="clear:both" />
| |
| * To assign the Boolean switches and displays to a node, click on the Boolean switch or light on the front panel then click on the node you wish to assign it to.
| |
| * If you make an error in a connection, right click the incorrect terminal and select ''Disconnect This Terminal''.
| |
| * The 8 nodes on the left side will be for the Boolean switches representing inputs showing occupancy for locations A-H. The 4 nodes on the bottom half of the icon starting from the left will be the inputs for locations I-L.
| |
| * Connect the 8 Boolean outputs that represent the orientation of the sector to the 8 nodes on the right side of the icon.
| |
|
| |
| {| class="wikitable" style="text-align:center; margin-left:auto; margin-right:auto"
| |
| |+align="bottom"|Figure 2: Node assignments of the student's digital logic circuit
| |
| |-
| |
| |Input<br />A
| |
| |rowspan="4"|
| |
| |rowspan="4"|
| |
| |rowspan="4"|No<br />Path
| |
| |rowspan="4"|Direction<br />of<br />Travel
| |
| |rowspan="4"|Top or<br />Bottom
| |
| |rowspan="4"|Reverse<br />Running<br />Mode
| |
| |Sector<br />1
| |
| |-
| |
| |Input<br />B
| |
| |Sector<br />2
| |
| |-
| |
| |Input<br />C
| |
| |Sector<br />3
| |
| |-
| |
| |Input<br />D
| |
| |Sector<br />4
| |
| |-
| |
| |Input<br />E
| |
| |rowspan="4"|Input<br />I
| |
| |rowspan="4"|Input<br />J
| |
| |rowspan="4"|Input<br />K
| |
| |rowspan="4"|Input<br />L
| |
| |rowspan="4"|
| |
| |rowspan="4"|
| |
| |Sector<br />5
| |
| |-
| |
| |Input<br />F
| |
| |Sector<br />6
| |
| |-
| |
| |Input<br />G
| |
| |Sector<br />7
| |
| |-
| |
| |Input<br />H
| |
| |Sector<br />8
| |
| |}
| |
|
| |
| *Replace the faded icon in the program ''Commissioning Test.vi'' with your digital logic VI. Right click on the icon and choose replace. Then choose ''Select a VI'' and find your VI. Replace it as shown in Figure 3.
| |
|
| |
| [[Image:Train9.jpg|frame|center|The program ''Commissioning Test.vi''
| |
| for students to insert their logic circuit]]
| |
|
| |
| * Before testing your digital logic circuit, turn on the power to the middle workbench where the two power supplies are connected.
| |
| * Continuously run the ''Commissioning Test.vi'' and ensure that the lights on the front panel accurately represent the presence or absence of a train.
| |
| * Flip the ''Reset'' switch up and down and the track will be preset to the specified orientation.
| |
| * Once those parameters are checked, test the digital logic circuit by flipping the ''Test Track'' switch.
| |
|
| |
|
| = Appendix C: Drop Down Selection Box = | | = Appendix C: Drop Down Selection Box = |
| ''In order to create and use a drop down selection box in your project, please closely read the following instructions that will aid you in creating and configuring the drop down box for use in your project:''
| |
|
| |
| # The very first step in the entire drop down box creation process is placing the to-be configured drop down control on the front panel of your VI. Go ahead and right-click anywhere on the front panel; select '''''Text Ctrls''''', followed by '''''Menu Ring'''''. You should now see a drop-down menu appear on the front panel, which should look similar to the following: [[Image:Train12.jpg|frame|none]]
| |
| # Next, we will need to add some appropriate selections to the drop-down box you created in the last step. These selections will facilitate multiple modes of the drop-down box and therefore let you control many different cases of one control structure. Right-click on your drop-down menu on the front panel, and click '''''Edit Items'''''. You should see a dialog box appear on the screen. Click on the insert button, and enter the name you will assign the TOP track. Hit the return key and enter the name you will assign the MIDDLE track. Repeat this process again for the BOTTOM track. After entering the bottom track, check to make sure that there are exactly three items entered. Your screen should look like the following: [[Image:Train13.jpg|frame|none]] Hit OK and your drop-down menu will have the correct settings to implement your digital logic.
| |
| # Finally, we want to use the drop-down menu to control a case structure. Create a case structure on the back panel and wire the drop-down menu to it. You will notice that there are currently only two different cases available in the case structure. We do not want this, as there are three different positions that the train can be placed on. Right click on the case structure and select '''''Add Case After'''''. This will create a third case, which is necessary for completing the digital logic for the train. You will notice that the three different cases are labeled 0, 1, and 2. Case 0 refers to the top track, case 1 the middle track, and case 2 the bottom track. '''''<span style="color: red">Do NOT change these labels to any text, your VI will not function if you do this. Your back panel will look similar to the following:</span>'''''[[Image:Train14.png|frame|none]]
| |
|
| |
| = Appendix D: Boolean Logic =
| |
| It is important to have a solid foundation in Boolean Logic when designing the RTGS system. The technique that is recommended for approaching this project is to '''create truth tables''', '''generate Kaurnaugh maps (K-maps)''', '''generate logical equations''', and '''simplify those equations'''. These simplified equations can be implemented using gates in the LabVIEW software. This guide presents a standard method for using this technique, it is highly recommended to read this entire section before beginning the project.
| |
|
| |
| == Truth Tables ==
| |
| A truth table is a chart which shows what happens under any circumstance for a logical device. Any logical system, that is a system which has binary (0’s and 1’s) input can be considered a '''finite state machine'''. This means that all the possible combinations of inputs can be known, and all the possible outcomes of those inputs can be plotted. The number of combinations of inputs can be determined by the number of input variables:
| |
|
| |
| <math style="display: block; margin: 0 auto;">\# combinations = 2^{\# variables}</math>
| |
|
| |
| Thus when we have 5 possible obstructions on the track, which can either be on or off, we have 2<sup>5</sup> possible combinations of those obstructions, which in this case is 32. This number tells you how many rows you must put in your truth table.
| |
|
| |
| When you begin writing your truth table, always start by writing all the input combinations. It is simple to calculate how many there should be, but to ensure each possible combination is included with no repeats, follow this procedure:
| |
| * We have an example logical system with 3 variables, thus there are 8 possible combinations of these 3 variables that we can have
| |
| * Each variable gets its own column in the table, in whatever order you like, as long as you keep track of it
| |
| * Starting with the rightmost column of inputs, write “0” in the first row of the table, then “1” in the next row, then “0”, then “1”, and so on, alternating the value of the column every row
| |
| * In the next column to the left, write “0” in the first two rows, then “1” in the next two rows, alternating the value every two rows
| |
| * In the leftmost column of our example table, write “0” for the first four rows, then “1” for the last four rows
| |
| * For systems with a greater number of variables, continue the pattern, doubling the number of rows before you alternate the value in each successive column
| |
|
| |
| {| class="wikitable" style="font-weight: bold; text-align: center; float: right;"
| |
| !A!!B!!C
| |
| |-
| |
| |style="background-color: rgb(109, 158, 235);"|0
| |
| |style="background-color: rgb(109, 158, 235);"|0
| |
| |style="background-color: rgb(109, 158, 235);"|0
| |
| |-
| |
| |style="background-color: rgb(109, 158, 235);"|0
| |
| |style="background-color: rgb(109, 158, 235);"|0
| |
| |style="background-color: rgb(224, 102, 102);"|1
| |
| |-
| |
| |style="background-color: rgb(109, 158, 235);"|0
| |
| |style="background-color: rgb(224, 102, 102);"|1
| |
| |style="background-color: rgb(109, 158, 235);"|0
| |
| |-
| |
| |style="background-color: rgb(109, 158, 235);"|0
| |
| |style="background-color: rgb(224, 102, 102);"|1
| |
| |style="background-color: rgb(224, 102, 102);"|1
| |
| |-
| |
| |style="background-color: rgb(224, 102, 102);"|1
| |
| |style="background-color: rgb(109, 158, 235);"|0
| |
| |style="background-color: rgb(109, 158, 235);"|0
| |
| |-
| |
| |style="background-color: rgb(224, 102, 102);"|1
| |
| |style="background-color: rgb(109, 158, 235);"|0
| |
| |style="background-color: rgb(224, 102, 102);"|1
| |
| |-
| |
| |style="background-color: rgb(224, 102, 102);"|1
| |
| |style="background-color: rgb(224, 102, 102);"|1
| |
| |style="background-color: rgb(109, 158, 235);"|0
| |
| |-
| |
| |style="background-color: rgb(224, 102, 102);"|1
| |
| |style="background-color: rgb(224, 102, 102);"|1
| |
| |style="background-color: rgb(224, 102, 102);"|1
| |
| |}
| |
|
| |
| Here is what the truth table should look like, with 0s and 1s colored differently to show the pattern:
| |
|
| |
| Note that this truth table only shows the inputs. The outputs have not been written in yet. They will occupy their own columns. When you design the RTGS logic, each obstacle will be an input column, and each switch will be an output column. When you are figuring out the logic of the RTGS, remember that it is very difficult to approach the system as a whole.
| |
|
| |
| Keep in mind what are some ways to approach the problem using Boolean logic? Which do not require a giant truth table?<br style="clear: both;" />
| |
|
| |
| == Karnaugh Maps ==
| |
| A Karnaugh map (K-map) is a diagram that aids the visualization of something called '''prime implicants'''. The term itself is less important and can be explained implicitly through the charts themselves. Essentially, we create K-maps to help see the simplified Boolean equation of a system directly without needing Boolean algebra. However, the K-map method is limited to systems with at most '''four variables'''. With five-variable or greater K-maps can get very complicated.
| |
|
| |
| When we draw a K-map, variables are grouped geometrically rather than in separate rows. Let’s begin with the simplest example, a 2-variable K-map. Our map takes the shape of a 2x2 square table, with variable “A” over the right two squares and variable “B” over the bottom two squares:
| |
|
| |
| {| class="kmap" style="margin: 1em auto;"
| |
| |-
| |
| !!!!!0!!1
| |
| |-
| |
| !!!!!<math>\overline{A}\,</math>!!<math>A\,</math>
| |
| |-
| |
| !0!!<math>\overline{B}\,</math>
| |
| |0||1
| |
| |-
| |
| !1!!<math>B\,</math>
| |
| |1||1
| |
| |-
| |
| |}
| |
|
| |
|
| The above Karnaugh Map shows the logic for the Boolean OR operation. The cells that the variable is superimposed over correspond to input rows from the truth table for when that variable is 1. In other words, variable “A” has a value of 1 when the input combination AB is 10 or 11. In the truth table for OR, 10 and 11 both output a value of 1. Thus both cells underneath “A” are marked with a 1. Likewise, “B” has a value of 1 when AB is 01 or 11. Both these combinations in the truth table have an output of 1 as well, so we mark the cells with a 1, noting that marking the cell corresponding to 11 is redundant. The top left cell, which corresponds to 00, has 0 as its output, so we do not mark the cell.
| | == == |
| | |
| You can think of the cells that are “covered” by each variable in the K-map as being the cells that correspond to when a variable or obstacle is “on”. The cells that are not covered are the input combinations for when that variable is “off”. The cells themselves each correspond to one output from the truth table. A K-map can only be made for one output variable at a time.
| |
| | |
| To obtain our Simplified Boolean Equation, we must circle groups of 1’s in our K-map and correlate them to logical statements. We can only circle adjacent 1’s and only in powers of two. Working with the K-map from above, we can circle the rightmost two 1’s and we can also circle the bottom two 1’s. In general, you should avoid circling the same cell more than once, however to generate maximum-sized circles, it is sometimes unavoidable. Now that we have our circles, we may now write the logical expression they represent:
| |
| | |
| [[Image:RTGS10.png|frame|none]]
| |
| | |
| Each individual circle is added to obtain the final Boolean equation. Thus, in our example, the circles add to make the statement A+B. Our Boolean equation is OUTPUT = A+B, which is simply the OR gate.
| |
|
| |
|
| == Boolean Algebra == | | == Boolean Algebra == |
| In general, it is easier to use the K-map to simplify truth tables that are relatively small (less than five variables). However, you may find the need obtain simplified expressions logical systems of a large number of variables, which requires Boolean algebra. In general, an unsimplified Boolean equation obtained directly from the truth table will contain one term for each 1 (maxterm) in the output variable. One equation can only define one output variable at a time. Let’s look at an example truth table of three input variables. We are primarily interested in the output column, which is highlighted in red. The output column values are arbitrary, we are trying to determine their logic:
| |
|
| |
| {| class="wikitable" style="text-align: center;"
| |
| !a!!b!!c!!out
| |
| |-
| |
| |0||0||0
| |
| |style="background-color: rgb(234, 153, 153);"|0
| |
| |-
| |
| |0||0||1
| |
| |style="background-color: rgb(234, 153, 153);"|1
| |
| |-
| |
| |0||1||0
| |
| |style="background-color: rgb(234, 153, 153);"|0
| |
| |-
| |
| |0||1||1
| |
| |style="background-color: rgb(234, 153, 153);"|1
| |
| |-
| |
| |1||0||0
| |
| |style="background-color: rgb(234, 153, 153);"|0
| |
| |-
| |
| |1||0||1
| |
| |style="background-color: rgb(234, 153, 153);"|1
| |
| |-
| |
| |1||1||0
| |
| |style="background-color: rgb(234, 153, 153);"|1
| |
| |-
| |
| |1||1||1
| |
| |style="background-color: rgb(234, 153, 153);"|1
| |
| |}
| |
|
| |
| So we see that the output, ''out'' has a value of 1 when ''abc'', in order, are 001, 011, 101, 110, or 111. Writing these in terms of variables (1 corresponds to ''a'', 0 corresponds to <math style="vertical-align: baseline;">\overline{a}</math> or any other variable), we get:
| |
|
| |
| <math>out = \overline{a}\overline{b}c + \overline{a}bc + a\overline{b}c + ab\overline{c} + abc</math>
| |
|
| |
| Boolean algebra is the process that helps us simplify our Boolean equation. Using a few rules, we can get the same “simplest” expression as we would with a K-map. There are many more rules to Boolean algebra, here is an abbreviated list:
| |
| #Substitution: Any variable listed in these rules may be substituted for a larger expression. e.g, let <math style="vertical-align: baseline;">k=m+pq\,\!</math>
| |
| #Identity: <math style="vertical-align: baseline;">k+0=k\,\!</math> and <math style="vertical-align: baseline;">k1=k\,\!</math>
| |
| #Distributive property of addition: <math style="vertical-align: baseline;">k+ \left ( mp \right ) = \left ( k+m \right ) \left ( k+p \right ) \,\!</math>
| |
| #Distributive property of multiplication: <math style="vertical-align: baseline;">k \left ( m+p \right )=km+kp\,\!</math>
| |
| #Cancellation property: <math style="vertical-align: baseline;">k+ \overline{k} =1\,\!</math> and <math style="vertical-align: baseline;">k \overline{k}=0\,\!</math>
| |
| #Another type of identity: <math style="vertical-align: baseline;">m+m=m\,\!</math> and <math style="vertical-align: baseline;">mm=m\,\!</math>
| |
| #Another type of cancellation: <math style="vertical-align: baseline;">m+1=1\,\!</math> and <math style="vertical-align: baseline;">m0=0\,\!</math>
| |
| #Repeated variables: <math style="vertical-align: baseline;">k+km=k\,\!</math> and <math style="vertical-align: baseline;">k \left ( k+m \right ) =k\,\!</math>
| |
| #Double inversion: <math style="vertical-align: baseline;">k=\overline{\overline{k}}\,\!</math>
| |
| #Associative property of addition: <math style="vertical-align: baseline;">k+ \left ( m+p \right ) = \left ( k+m \right ) +p=k+m+p\,\!</math>
| |
| #Associative property of multiplication: <math style="vertical-align: baseline;">k \left ( mp \right ) = \left ( km \right ) p=kmp\,\!</math>
| |
| #Redundancy: <math style="vertical-align: baseline;">k+ \overline{k} m=k+m\,\!</math> and <math style="vertical-align: baseline;">k \left ( \overline{k}+m \right ) =km\,\!</math>
| |
| #NAND and NOR principle: <math style="vertical-align: baseline;">\overline{k+m}=\overline{k} \overline{m}\,\!</math> and <math style="vertical-align: baseline;">\overline{km}=\overline{k} +\overline{m}\,\!</math>
| |
| #One useful simplification: <math style="vertical-align: baseline;">km+\overline{k} p+mp=km+\overline{k} p\,\!</math> and <math style="vertical-align: baseline;">\left ( k+m \right ) \left ( \overline{k}+p \right ) \left ( m+p \right ) = \left ( k+m \right ) \left ( \overline{k}+p \right ) \,\!</math>
| |
| #Order of Operations: PNAO: Parentheses, NOT, AND, OR
| |
|
| |
| One of the first simplifications that can be made to the equation above is to factor out c from the first three terms and the last one. Like in regular algebra, Boolean variables can be factored when they share the same value across multiple terms. [Rule 3] We now have:
| |
|
| |
| <math>out = c \left ( \overline{a}\overline{b} + \overline{a}b + a\overline{b} + ab \right ) + ab\overline{c}</math>
| |
|
| |
| In fact, we can factor the expression within the parentheses even further:
| |
|
| |
| <math>out = c \left [ \overline{a} \left ( \overline{b} + b \right ) + a \left ( \overline{b} + b \right ) \right ] + ab\overline{c}</math>
| |
|
| |
| Look at the statement within the inner parentheses. When we read out the first and last terms, the statement is true whether b is false or true. [Rule 5] Thus we may rewrite <math style="vertical-align: baseline;">b+\overline{b}</math> as 1, and the whole statement in the brackets becomes:
| |
|
| |
| <math>out = c \left [ \overline{a}1 + a1 \right ] + ab\overline{c}</math>.
| |
|
| |
| When any variable is in an AND statement with 1, it becomes just the variable alone. [Rule 2] The result solely depends on the variable.
| |
|
| |
| <math>out = c \left [ \overline{a} + a \right ] + ab\overline{c}</math>.
| |
|
| |
| Again, we apply Rule 5 on ''a'' to get <math style="vertical-align: baseline;">out = c 1 + ab\overline{c}</math>. Rule 2 can be applied again.
| |
|
| |
| <math>out = c + ab\overline{c}\,\!</math>
| |
|
| |
| The statement is close to completely simplified, but there is still one more step. In the second term, there is a <math style="vertical-align: baseline;">\overline{c}</math> multiplied with ''ab''. This <math style="vertical-align: baseline;">\overline{c}</math> is superfluous because the term ''c'' is already in our expression. In other words, any combination involving ''c'' has already been accounted for, thus the remaining terms in the equation will work independently of ''c''. [Rule 12] Our simplified Boolean equation is:
| |
|
| |
|
| <math>out = c + ab\,\!</math>
| |
|
| |
|
| Note that terms are independent of the order of their arguments, meaning that we can rearrange variables in an equation and still mean the same thing. [Commutative property] | | Note that terms are independent of the order of their arguments, meaning that we can rearrange variables in an equation and still mean the same thing. [Commutative property] |