MATLAB Skill Builder
| This page's accuracy may be compromised because of out-of-date information. The information displayed on this page has been deprecated and is kept for historical purposes only. There may or may not be information relevant to the current course curriculum. |
Objective
In this exercise, you will be introduced to additional software used by technical professionals. You will learn a basic analytical software package, Matlab
Introduction to Matlab
Starting Matlab:
Open Matlab.
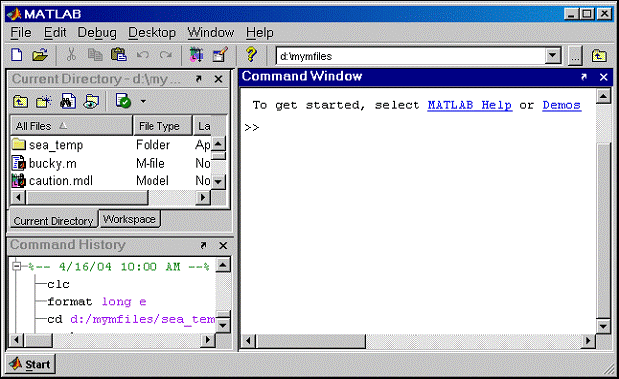
Matlab Desktop:
Command Window: The command window is the window you write commands in to perform desired Matlab functions.
Current Directory: The current directory window shows which directory Matlab is currently using. It can be replaced by the workspace window.
Workspace: The workspace widow displays the names and the values of the variable you are currently using in the Matlab workspace.
Command History: The command history window displays the commands that you have recently used in the Matlab command window. This also displays commands from previous Matlab sessions.
Basic Arithmetic:
- Open the workspace window, it should be empty.
- In the command window type 3 + 5 and press enter. This code adds the numbers 3 and 5.
- Type a = 7 + 6; in the command window, remember to include the semicolon after the expression. The semicolon supresses the output to the screen. You should use this for all your commands after basic trigonometry.
- Now type the letter "a" in the command window and press enter. By simply typing the letter "a" you can display the value of "a."
- Enter b = 16 – 4 this command subtracts 4 from 16
- Enter c = 7 * 6 this command multiplies 7 and 6
- Enter d = 25 / 5 this command divides 25 by 5
- Enter e = 8 ^ 2 this command raises 8 by the power of 2 or 82
- Enter f = sqrt(36) this command returns the square root of 36
- Enter A = [ 4 8 15 16 23 42 ] this command creates a vector consisting of the numbers 4, 8, 15, 16, 23 and 42
- Enter B = [ 13 7 82 5 19 8 ]
- Enger C = A + B this command adds the vectors A and B
- Enter D = B – A this command subtracts the vector A from B
- Enter E = A .* B this command multiplies A and B element-by-element; if the symbol "*" is used the multiplication will not be element-by-element, it will be matrix multiplication
- Enter F = B ./ A this command divides B by A element-by-element
- Enter G = B .^ 2 this command raises each element of the vector B by the power of 2
- Enter H = sqrt(A) this command returns the square root of each element of the vector A
- Enter I = 0:10 this returns a vector consiting of the numbers 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 and 10
- Enter J = 0 : 0.5 : 5 the increments between 0 and 5 are 0.5
- Enter K = 25 : 5 : 53
- Enter L = 100 : -3 : 80
- Enter M = [16 3 2 13; 5 10 11 8; 9 6 7 12; 4 15 14 1] this creates a matrix
- sum(M) this function adds all of rows together by column; it is a good example of how Matlab can perform many functions at the same time
Note: Matlab can perform multiple operations on series of numbers, or matrices. These tools are very useful in advanced mathematics such as Linear Algebra.
Note: The ":" operator counts between two different numbers. By default the increment value is "1" though this can be changed.
Basic Trigonometry:
- In the command window type the word "clear"; this clears the workspace of the variables that you have been using
- Enter x = π/2 and y = sin(x)
- Enter y = cos(π)
- Enter x = π/4 and y = sin(x)
- Enter y = cos(x)
Note: In Matlab π is represented by the word "pi."
2-D Plotting:
- In the command window type the word "clear"
- Enter x = 0 : π/8 : 2*π and y = sin(x)
- Enter plot(x, y), creates a plot of x against y. Save this plot as "EG sin"
- Now plot x against y = cos(x), save this plot as "EG cos"
- Enter theta = 0 : π/16 : 2*π;
- Enter x = cos(theta); and y = sin(theta);
- Again, plot x against y and save this as "EG circle"
- Enter x = 0 : 5; and y = exp(x);
- Again, plot x against y and save this plot as "EG e"
Note: exp(x) represents ex
3-D Plotting:
- In the command window type the word "clear"
- sphere(20) this creates a three-dimensional figure of a sphere. Save this as "EG sphere"
- Click onto the rotation tool on the top of the window
- Click on the figure and drag the mouse around the screen
- Enter z = 0 : 0.1 : 2 and r = sin(3*π*z) + 2; this makes z equal to the space in between zero and two at increments of 0.1
- Enter cylinder(r) save this as "EG cylinder"
- In the command window type the word "clear"
- Enter u = -5 : 0.2 : 5; [x, y] = meshgrid(u,u); this changes the format of the data so it can be used in three-dimensional plots
- To demonstrate your new found knowledge of Matlab use what you
have learned to write
in Matlab code. Remember that x and y are vectors and they need to be evaluated element-by-element. - Enter surf(x,y,z) this creates a three-dimensional plot of the function z(x,y). Save this as "EG surface"
- Copy and paste your Matlab command history into a Word Document. Copy your Matlab graphs and paste them into the same Word Document underneath the code history you used to make them.
- Exit Matlab by clicking on the red "x" on the upper right hand corner of the window
- Submit this Word document to eg.poly.edu. Remember to include a cover page when you submit.
You have now completed the lab. Log off the PC and make sure your work area is clean, with any scrap paper you used, etc. properly of.
| This page's accuracy may be compromised because of out-of-date information. The information displayed on this page has been deprecated and is kept for historical purposes only. There may or may not be information relevant to the current course curriculum. |

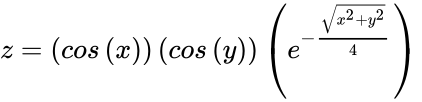 in Matlab code. Remember that x and y are vectors and they need to be evaluated element-by-element.
in Matlab code. Remember that x and y are vectors and they need to be evaluated element-by-element.