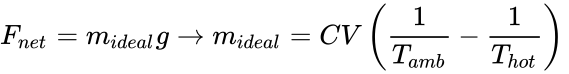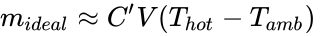Engineering Considerations
The following provides more detail than is typically seen in the labs. What we have tried to do is explain and show how the engineering design process works. The concepts are different in each lab, but the approaches have similarities. It is not that there is a unique method or a unique solution, but rather there is a logical phenomena/concept based approach.
Why Develop a Set of (Simple) Equations?
In a engineering problem — if one wants to understand how to develop a good engineering solution, and even better (if possible), an optimum solution, then one must understand what the variables are and how they impact the performance. The degree to which this is possible will depend on the problem.
And while you may not be able to independently arrive at all of the equations developed (reach closure where you have, for example 3 equations and 3 unknowns, and solve them), the equations/methodology should be one that makes sense--one you can follow. Basically writing equations instead of a word description and some useful and realistic approximations.
Developing a Suitable (More Optimum) Design
As guidance for future labs, developing an understanding of the concepts involved guides you in the engineering solution. And ideally the concepts can be replaced by a set of equations. Actually this is why there is generally an overview/theory section to a lab.
Another major aspect of developing/engineering a design/solution is building on past designs and/or one's intuition (mind's eye) understanding of the problem. This also explains why the lab reports generally have an introduction with a history and other examples/applications. Understanding the processes at work and combining this with the past designs — one can develop a better solution.
Actually as part of the "brainstorming process," which is the groups collectively doing some of what is described above, other partially related ideas may come to mind.
Developing the Ideal Hot Air Balloon Payload Capacity
It turns out the hot air balloon design — at least as regards initial payload lifted (not how long) — is amenable to a reasonably simple analysis and the process is shown herein.
Clearly you could say: " making the hot air 40 °C hotter than ambient, as compared to 20 °C hotter, will mean a greater payload capability," and even nicer is an equation that allows you to say how much greater! For an "ideal" hot air balloon (defining an ideal balloon as one with zero structural mass) the equations will show it will be double the payload.
And since the structural mass will clearly not be insignificant, the equations could in principle be further developed (or the components of the completed balloon weighed). That will not be done here (we would need more physical information/data, but it is pretty clear the balloon shape that has the minimum surface area-to-volume can be identified, and thus the lowest structural mass-to-volume. Of course it is not so simple since it has to be built solely with the materials given in this lab., and must be stable enough to hold the hot air for some period of time.
As an example of brainstorming (and a hint!) although kites do not use Archimedes' Principle they are somewhat related to hot air balloons. So why does a (traditional) kite have a long tail? And what does this have to do with the design of a hot air balloon?
Actually from this discussion you already have some guidance to develop a better hot air balloon. The problems to be addressed include: (1) What maximizes payload? (2) What minimizes structural mass? (3) What has greater hydrodynamic and structural stability? Actually these relate directly to the competition ratio: Balloon Competition Ratio = (1) payload x (2) time aloft / (3) cost.
If we wanted to say how good is our design--as regards initial payload lifted--we could actually arrive at a percenatage. e.g., a design lifted 10% of the ideal case. Clearly this is useful--if the hot air balloon lifted 80% of the maximum possible, then design improvements should likely look at other improvements--reducing the cost 30% or increasing the time aloft by 30% would be more meaningful (look at the balloon competition ratio!).
A related item occurs when comparing your lab. results to the winning design. Students often fail to realize they can quantify how large an improvement would be gained by changing something. Again--look at the applicable competition ratio (or whatever it is called)--and do the numbers!
In our analysis, above, the buoyant force equation was developed (Fnet = midealg = (ρamb–ρhot)Vg); however, we don't measure density. We can measure the hot air temperature, the ambient air temperature, and (although not very precise) we can estimate the balloon volume. Using the equation for gas density (ρ = C / T), and if we assume the balloon structural mass is negligible (an idealized case), the payload mass lifted (mideal), can be found.
and now we will make a typical and useful engineering approximation (which is realistic for (Thot) and (Tamb) not too different, as is our case). It is easily shown, the equation is (approximately), (mideal ≈ CV/Tamb2 (Thot – Tamb)), or
where the ambient air temperature and heated air temperature are (Tamb) and (Thot), respectively (both in °C), the constant C' is (about) 0.0040 (kg/m3)/ °C, or 4.0 (g/m3)/ °C , and the (mideal) is the payload for a hot air balloon of zero structural mass.
If we specify the balloon volume (V) is 1 m3, the maximum allowed for this lab, the payload is proportional to the hot-to-ambient air temperature difference (as we may have expected), and for 1 °C hotter air 4.0 grams (or 4 paper clips) can be lifted, and for a 20 °C hotter air 80 grams (or 80 paper clips). (Caution--these masses (number of paper clips are for an ideal (weightless) 1 m3 balloon--and are an order of magnitude larger than lab. experience might suggest!)
Finally it is useful to note that the approximation used above [to get (mideal≈C'V(Thot–Tamb))] is not needed--more complicated (non linear) equations (such as the Ideal Gas Law) are readily solved by electronic calculator or computer; however, the physical insights are not as obvious. In this sense often an approximate answer is more useful than a more exact answer!