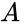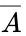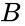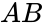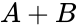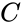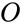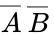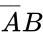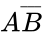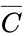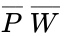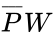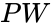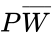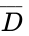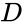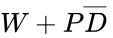Difference between revisions of "Digital Logic"
(added O= to make an expression an equation) |
(→Individual Lab Report: 2014-01-09 Roger Avendano) |
||
| Line 231: | Line 231: | ||
<li>Describe the design changes that would be necessary if one of the barns used a bell as | <li>Describe the design changes that would be necessary if one of the barns used a bell as | ||
an alarm and the other used a horn.</li> | an alarm and the other used a horn.</li> | ||
<li>Describe how the final combinational logic circuit was obtained | |||
<li>Insert a screenshot of the front and back panels in the report | |||
</ul> | </ul> | ||
Revision as of 09:28, 16 January 2014
OBJECTIVES
The experimental objective of this lab is to design a combinational logic circuit that will activate under specific conditions and test it using LabVIEW. After testing, it will be built on the NI-ELVIS II+ prototyping board.
Your goal is to become familiar with the principles of digital logic and digital logic circuits. Understanding how logic gates work is critical to this process.
OVERVIEW
The first step in understanding the digital circuits that control the function of electronic devices is the mastery of Boolean logic. George Boole, an English mathematician, established modern symbolic logic in 1854 with the publication of his paper, "Laws of Thought." Now called Boolean algebra, it is the foundation of digital circuitry. Boole's method of logical inference enables us to draw conclusions from any proposition involving any number of terms. Boolean logic demonstrates that our conclusions are logically contained in our original premises.1
In Boolean logic, there are only two values, true and false, represented by the numbers 1 and 0, respectively. These values are combined in equations to yield results that also have these two values. The equations are represented by truth tables that show the inputs to the equation and the outputs produced for those inputs. The rows of the table contain all the possible combinations of 1s and 0s for the inputs. The number of rows is determined by the number of possible combinations.
Boolean logic is applied to digital circuitry through the use of simple logic gates. There are symbols for each of these types of gates, and the connections between them are represented by lines running from the output of one gate to the input of the other. A line can connect only one output to each input. There are seven of these gates: the NOT, AND, OR, NAND, NOR, XOR, and XNOR gates. We will limit our discussion to the first three.
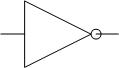
The NOT gate is the simplest of these three. It is an inverter. It takes one only input and produces its opposite as output. Its symbol looks like this:
The truth table for a NOT gate has one input, which we'll call A, and one output. The symbol for the operation is a horizontal bar over the variable, so the truth table looks like this:
| 0 | 1 |
| 1 | 0 |
The AND gate performs an and operation on its inputs. Like English, if all the inputs are true, then the output is also true. However, if either of the inputs is false, then the output is also false. An AND gate can have two or more inputs, but for this lab, we'll only use two inputs. The symbol for an AND gate looks like this:
This gate has two inputs, which we'll call A and B, and one output. The symbol for the AND operation is a dot(·) or just has the two inputs one after the other with nothing between them. The truth table looks like this:
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
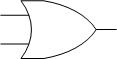
Finally, the OR gate performs an or operation on its inputs. Like English, if either of the inputs is true, then the output is also true. However, if ALL the inputs are false, the output is also false. An OR gate can have two or more inputs, but for this lab, we'll only use two inputs. The symbol for an OR gate looks like this:
This gate has two inputs, which we'll call A and B, and one output. The symbol for the OR operation is a plus(+). The truth table looks like this:
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
The truth table attached to each of these gates indicates the circumstances under which the gate will return a value of true. We'll use these tables to write a Boolean equation for our problem. All the combinations that yield an output of 1 are kept, and the equation is written. This is called a Sum of Products solution.
Note: If we use zeroes instead of ones, we'll get a Product of Sums solution, which is beyond the scope of this description.
We can make a Boolean equation that is a solution to a problem in digital logic by forming a truth table of our own, where we show every possible combination of inputs and what their corresponding outputs should be. Once that is accomplished, we will simplify our equation using a Karnaugh Map (K-Map). This tool is used to devise a simplified Boolean equation which identifies and removes all the conditions that do not contribute to the solution. This final equation is the one used to build the digital circuit, and will be a combination of the gates described above.
A K-Map is a two dimensional representation of the truth table that allows us to see common characteristics of the inputs, and allows us to simplify the digital logic which would implement the truth table. For an equation with three inputs, we usually show the all the combinations of first two inputs as four columns, and the third input values as two rows. For four inputs, we would show all the combinations of the third and fourth inputs as four rows. Only one value can change at a time in adjacent rows or columns. For example, consider the following truth table, where A, B, and C are the inputs and O is the output:
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
This table looks complex, but it can be simplified. We'll make the K-Map for this truth table:
| 0 0 | 0 1 | 1 1 | 1 0 | ||
|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 0 | |
| 1 | 1 | 1 | 1 | 1 |
Next, we'll look for cells that have things in common. For example, the entire bottom row has ones in all its cells. This means that any time C is true, the output is true. We can do this in a more organized manner. Look for cells that form rectangles, where the number of cells in the rectangle is a power of 2: 1, 2, 4, 8, etc. The bottom row is an example of this. If you look further, you'll see another small rectangle of 2 cells in the column with 1 1 at the top. What this means is that the ouput is true whenever A and B are true. The rectangles are allowed to overlap, so you might use the same cells more than once, which happened here. You should look for the biggest rectangles first, and keep finding smaller retangles until all the cells with a 1 in them are used. This means that sometimes just single cells will remain at the end. In this case we were lucky because we could cover all the cells containing a a with just these two rectangles.
What this means is that if the conditions for either rectangle are true, the output will be true. Looking at the row and column labels, the bottom row is C, and for the colum, the header is AB. This leads to the simplified Boolean equation:
O = AB+C
This equation meets the conditions in the truth table, and achieves the desired result with the minimum number of logic elements.
YOUR ASSIGNMENT
Individual Lab Report
Follow the lab report guidelines laid out in the page called Specifications for Writing Your Lab Reports in the Technical Communication section of this manual. As you write, the following discussion points should be addressed in the appropriate section of your lab report:
- Describe the problem you are solving in your introduction.
- Describe how AND, OR, and NOT gates work.
- What is a truth table? How does it contribute to obtaining a Boolean equation?
- What is a K-map? How does it to contribute to obtaining a simplified Boolean equation? To demonstrate the simplification, show what the equation would look like if you used wrote terms for each of the true values, and the simplified equation by applying the K-Map. Discuss how much simpler the circuitry would be by applying K-Maps.
- Describe how a digital logic circuit is built using these tools.
- Was the experiment a success? If failure, why?
- Compare the problem before and after it was simplified
- Why is there a need for the minimization of a logic design and what are the advantages?
- How does the use of a combinational logic circuit contribute to advances in technology?
- Describe the design changes that would be necessary if one of the barns used a bell as an alarm and the other used a horn.
- Describe how the final combinational logic circuit was obtained
- Insert a screenshot of the front and back panels in the report
Team PowerPoint Presentation
Follow the presentation guidelines laid out in the page called EG1003 Lab Presentation Format in the Introduction to Technical Presentations section of this manual. When you are preparing your presentation, consider the following points:
- How does digital logic impact the world today?
- If you can look into the future, how will digital logic change the world?
MATERIALS AND EQUIPMENT
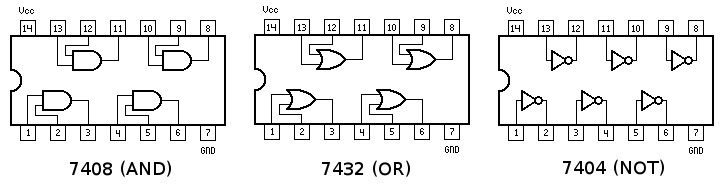
- 7432 IC (4 dual-input OR gates)
- 7408 IC (4 dual-input AND gates)
- 7404 IC (6 single input NOT gates)
- Lab PC with LabVIEW Software
- NI-ELVIS II+ with Prototyping Board
- Appropriate Wiring
Remember: You are required to take notes. Experimental details are easily forgotten unless written down. EG Standard Note Paper can be downloaded and printed from the the EG Web site. Use your lab notes to write the Procedure section of your lab report. At the end of each lab your TA will scan your lab notes and upload them to the Lab Documents section of the EG Website. You must attach your lab notes at the end of your lab report (use the "Insert Object" command in MS Word after your Conclusion). Keeping careful notes is an essential component of all scientific practice.
SAMPLE PROBLEM
Problem Statement
An ATM has three options: to print a statement, withdraw money, or deposit money. The ATM will charge you $1 if you:
- Want to withdraw money,
- Want to print a statement without depositing money
- Truth Table: The inputs here are what you can do with the ATM. Let a variable P stand for printing a statement, W for withdrawing money, and D for depositing money. There is one output, which is whether or not the ATM session has a cost. Call the output C. We'll now take all the combinations of the inputs and show the corresponding outputs:
- Boolean Equation The combinations that yield an output of 1 are kept. Our approach will be, for each output of 1, to determine the input values and to AND those variables together. If an input is true, it can be used as is. For an input that is false, we'll invert it using the horizontal bar NOT operation we defined above. Since the output is true if any of the input condition combinations are true, we'll form the result by using an OR operation on all the terms formed by the AND operations. The following Boolean equation is created:
- Karnaugh Map (K-Map): Begin by drawing a table like the one below that maps out all the possible combinations. When deciding where to place each of the letters, keep in mind that you can only change one variable at a time between adjacent columns. For this example, the columns will chage from 00, to 01, to 11, to 10, as shown in Figure 2. Your TA will explain this further. The cells that are true are grouped in boxes of 2, 4, or 8 cells. This allows us to see what these cells have in common, and use that for the simplified Boolean equation. The K-Map in Figure 2 corresponds to the Boolean equation we just created.
- Simplified Boolean Equation: Next, we try to form the biggest boxes we can of 2, 4, and 8 cells. In the middle of Figure 3, you can see a box of four cells (2 rows by 2 columns), plus an overlapping box of two cells (1 row by 2 columns).
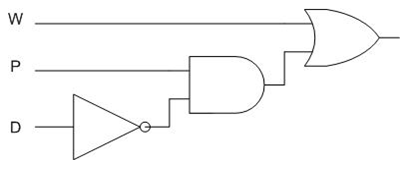
- Combinational Logic Circuit: We can now construct a logic circuit from the simplified equation. Looking at the equation, we can see that if we perform a NOT operation on D, and do an AND operation on the result and P, we get the second term in the equation. Then, if we take this result and do an OR operation with W, we get the overall result.
| Inputs | Output | ||
|---|---|---|---|
| P | W | D | C |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
In the above table 1=true (on), 0=false (off)
Inputs: P=print, W=withdraw, D=deposit
Output: 0=false (do not charge), 1=true (charge $1.00)
You should compare this equation with the truth table to make sure you understand how this works.
You should compare this K-Map with the equation to see why some cells are 1 and the others are 0.
| 0 0 | 0 1 | 1 1 | 1 0 | ||
|---|---|---|---|---|---|
| 0 | 0 | 1 | 1 | 1 | |
| 1 | 0 | 1 | 1 | 0 |
| 0 0 | 0 1 | 1 1 | 1 0 | ||
|---|---|---|---|---|---|
| 0 | 0 | 1 | 1 | 1 | |
| 1 | 0 | 1 | 1 | 0 |
Note: Always try to group the greatest number of neighbors in powers of 2.
To create a simplified Boolean equation, you must first group all the combinations together and eliminate those that contain both values of a variable. For example, for the big box in the middle, W is always true, but the box includes both the true and false values of P and D. This means that if W is true, the values of P and D don't matter since all their combinations are included. Similarly, for the small box, if P is true and D is false, the value of W doesn't matter since both its true and false values are included in the box. Putting this together, if W is true, or P is true and D is false, the output should be true, and this covers all the input conditions required to make a true output. We can now write this as a simplified Boolean equation:
As you can see, this equation is much simpler than the equation we started with, but is fully equivalent to it.
This is shown in Figure 4.
PROCEDURE
Problem Statement
A farmer owns a 350-acre dairy farm in upstate New York. In addition to milk and butter, the farmer sells fresh eggs at the Union Square Greenmarket in Manhattan. It is imperative that the farmer protects the hen that lays his golden eggs.
He has two barns, one hen, and a supply of corn. A fox has been attempting to eat the hen by hiding in a barn. The hen can move freely from one barn to the other. Farmer Georgi sometimes stores corn in one barn, and sometimes in the other, but he never stores it in both at the same time. The hen would like the corn; the fox would like to eat the hen. Farmer Georgi has hired you to design an alarm system that uses digital logic circuits to protect the hen and the corn. Your design should use the fewest gates and input variables possible. The alarm will sound if:
- The fox and the hen are in the same barn, or
- The hen and the corn are in the same barn.
Finding a Solution
Note: The two barns must be assigned a numeric equivalent before you prepare your truth table for Step 1. For example, use 1 for Barn 1 and 0 for Barn 2. For the alarm output, use 0 to indicate the alarm should be off, and 1 to indicate that the alarm should be on.
- On a sheet of lined lab note paper from the EG Web site, create a truth table that includes three inputs and one output. Assign the input variables. Make sure you include all possible scenarios for the hen, the corn, and the fox.
- Compute the output column. To do this, analyze the three inputs and determine whether the alarm would sound in each scenario. Place a 1 in the output column if the alarm will sound and a 0 if it will not.
- Note all the combinations that produce a 1 in the output column.
- Create a Boolean equation from this table that includes each of the inputs that produced a positive output.
- Create a K-Map. Draw a map that lists all the possible combinations. Use the Boolean equation to fill in the 1's on the K-Map.
- Circle the pairs of 1's. The 1's may only be circled in powers of 2 starting with the largest possible combination and working down to the smallest. The unfavorable outcomes are discarded.
- This process yields the simplified Boolean equation. Write this simplified equation down.
- Draw a schematic diagram of your simplified Boolean equation.
- Have your TA sign your work.
- After you have created your circuit, it must be tested. Build the circuit in LabVIEW. Make sure you use your simplified Boolean equation. Open LabVIEW and select New VI. Pull down the Window menu, select Tile Left and Right.
- Place three switches on the front panel that represent the hen, the corn, and the fox. Place one Boolean indicator to represent the output.
- Open the Functions palette. Select Boolean and choose the AND, NOT, and OR gates necessary for your circuit. Your TA will assist you in this process.
- Once you have completed your LabVIEW program, have your TA check your work.
- Now we will build the circuit on the Prototyping Board.
- On the board, identify each of the three black chips as an AND, OR, or NOT gate. To do this, read the number on the chip itself and match it with the list in the Materials and Equipment section of this lab. Use the pinouts in Figure 5 to wire your gates. You can tell that you are using the proper end of the chip by looking for the notch at one end, and match it to diagrams in Figure 5.
- Before we begin, we must connect our gates to a power supply and ground them. Insert one end of the wire into a hole on Row 54 (marked +5V) of the side breadboards. Insert the other end of the wire into the hole on the breadboard nearest pin 14 on the gate. Repeat this process for all three gates.
- The leftmost and rightmost columns of slots (the ones in between the red and blue lines) are connected vertically.
- The rest of the breadboard is connected horizontally; however, there is a break that runs down the center of the breadboard, separating Columns A-E and F-J as shown in Figure 6.
- Ground the circuit using the same method. Insert one end of a wire into a hole on Row 53 (marked ground) of the small breadboards, and the other end into pin 7 of the logic gate. Repeat this process for all three gates.
- If you look at the top right corner of the breadboard, you’ll find the Digital Input/Output (DIO) holes. Select one of the DIO row of holes to use as one of your variables and begin wiring the circuit based on your simplified Boolean equations. Assign the other DIO rows for the remaining variables.
- Continue this process until you have wired the entire circuit. Insert one end of the wire into the final output of your simplified Boolean equation. Attach the other end to any hole marked LED on the board.
- Plug in the NI-ELVIS II+ and connect the USB cable to the Lab PC.
- Power on the NI-ELVIS II+ by toggling the switch on the back of the device. When the pop-up window appears, select NI-ELVISmx Instrument Launcher and click OK.
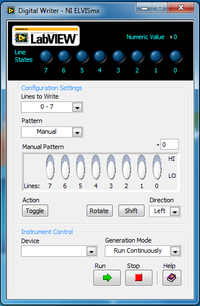
- Click on the DigOut Icon on the Instrument Launcher window.
- Select the appropriate range for the Lines to Write setting in the Digital Writer dialog window that corresponds to the DIO rows you chose. For example, if you have fox, hen, and corn on DIO 21, DIO 22, and DIO 23, then you would want to select 16 – 23.
- Click Run and toggle the switches corresponding to fox, hen, and corn. If you have any issues, ask your TA for help.
- Have your TA check your circuit.
The Breadboard is set up in the following manner:
Your lab work is now complete. Please clean up your workstation. Return all unused materials to your TA. Refer to section 3 Your Assignment for the instructions you need to prepare your lab report.
Footnotes
1 Boole, George, Encyclopedia Britannica, 2003. Encyclopedia Britannica Online. Retrieved July 29th, 2003 http://www.britannica.com/eb/article?eu=82823