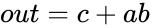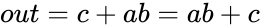Kaylee NRC
Introduction and Overview
Prerequisite
Specifications
Task
Cost Estimate
You will need to create a cost estimate using quotes from a reputable vendors. You are not limited to these vendors. When doing your cost estimate, be sure to include specification sheets from the vendors.
Create a cost estimate on a Microsoft Excel spreadsheet. The cost estimate should include the following:
- Labor cost breakdown with hours and rates
- All chips should be itemized with quantity, price per chip, and total cost per chip type
- No decimal places; this is an estimate after all. Round appropriately
- Total cost must be shown in the bottom right corner
Milestones, Benchmarks, and Deliverables
As work is done on the project, three Milestone presentations will report on the project's progress. All of the items assigned in each phase of the project are called Benchmark deliverables. These deliverables often consist of a combination of written submissions, presentations, and demonstrations. Benchmark assessments evaluate the progress of the project.
Preliminary Design Investigation
The Preliminary Design Investigation (PDI) is extremely important, as it lays the groundwork for the project. It outlines the project idea, inspiration, and goals.
The PDI must include:
- Cover Page
- Project Overview
- Goals & Objectives
- Design & Approach
- Cost Estimate
- Project Schedule
- Relevant Pictures
An example PDI template can be found here. The PDI is due by Benchmark A. Do not forget to include the items listed above. Use this link to access the VEX PDI Rubric.
Milestone 1
Prepare a preliminary assessment of the track system using digital logic (truth table, Karnaugh maps, and Boolean equations), a cost estimate, and an MS Project plan.
Look Ahead: What tasks are planned between now and Milestone 2?
See How To Give a Milestone Presentation for the format of a Milestone presentation.
Milestone 1 Deliverables:
- Presentation:
- Project description
- Design approach
- Mission statement
- How will the logic be implemented? (by inspection, partition, truth tables, etc.)
- Cost estimate
- MS Project schedule
- Progress update: current state of the project
Presentation notes:
- Be sure to include any special features and benefits of your design.
Introduction to NRC Programming
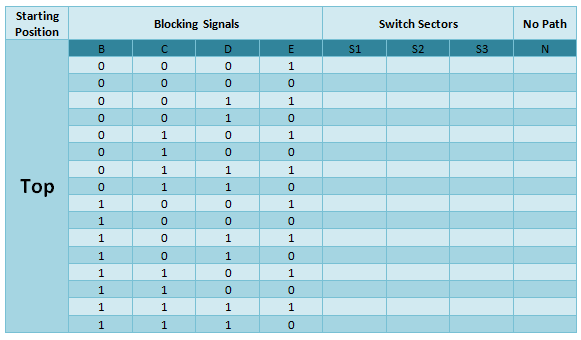
| Legend | ||
|---|---|---|
| Blocking Signals (B, C, D, E) | 0 | Free of obstacles |
| 1 | Blocked | |
| Switch Sectors (S1, S2, S3) | 0 | Straight |
| 1 | Cross | |
| No Path (N) | 0 | Train can proceed |
| 1 | Train CANNOT proceed | |
Benchmark Assessment A
- Direction of Travel: Left-To-Right
- Travel Mode: Normal
- Starting Positions: L1, L2, L3
- Sectors: 2, 4, and 6 (Keep in mind that since S1 is disabled in Normal mode, the L1 starting position creates a "No Path" condition regardless of any track conditions.)
- Total Number of Boolean Equations: (L2 S2, L2 S4, L2 S6, L3 S2, L3 S4, L3 S6, L2 No Path, L3 No Path) &mdashl; 8 equations
- Direction of Travel: Left-To-Right
- Travel Mode: Reverse
- Starting Positions: L1, L2, L3
- Sectors: 1, 2, 3, 4, 5, and 6
- Total Number of Boolean Equations: ( L1 S1, L1 S2, L1 S3, L1 S4, L1 S5, L1 S6, L2 S1, L2 S2, L2 S3, L2 S4, L2 S5, L2 S6, L3 S1, L3 S2, L3 S3, L3 S4, L3 S5, L3 S6, L1 No Path, L2 No Path, L3 No Path) &,dash; 21 Equations
Here are the Boolean variables you will need to create the equation. Many of the conventions have stayed the same from Milestone 1 and will stay the same until completion of the project:
- Let T represent the track that the train is on at the terminal. As before T can take on 3 possible values, Top, Middle, and Bottom.
- Let C represent a train blocking input C.
- Let D represent a train blocking input D.
- Let E represent a train blocking input E.
- Let F represent a train blocking input F.
- Let G represent a train blocking input G.
- Let H represent a train blocking input H.
- If C, D, E, F, G, or H = 0, the corresponding track is free of obstacles. If C, D, E, F, G, or H = 1, the corresponding track is blocked.
- Let S1 represent the status of the switch at Sector 1. Let S2 represent the status of the switch at Sector 2. Let S3 represent the status of the switch at Sector 3. When S1, S2, or S3 = 0, the train goes straight through. When S1, S2, or S3 = 1, the train crosses over on to the other track.
- Let N be the "No Path" condition and represent whether or not you can proceed through the switches to one track or another. When N=0, the path is clear, and the train can proceed. When N=1, all paths are blocked, and the train cannot proceed through the track by utilizing any combination of switched tracks.
C:\SLDP Railroad Train Guidance System\Benchmark Assessment A.vi
on the PC connected to the train layout. Your TA will test your VI by running your program with various combinations of tracks being blocked.
Milestone 2
Look Ahead: What tasks are planned between now and Milestone 3?
See How To Give a Milestone Presentation for the format of a Milestone presentation.
Milestone 2 Deliverables:
- Presentation:
- Project description
- Design approach
- Design changes since Milestone 1
- Mission statement
- Samples of logic design
- Truth tables
- Karnaugh maps
- Boolean equations
- VI interface (front and back panels)
- Cost estimate (previous and current). What changes were made?
- MS Project schedule (previous and current). What changes were made?
- Progress update: current state of the project (time, budget, etc.)
Benchmark Assessment B
Your VI will interface with the RTGS test track by using a custom VI provided by EG. It is located at
C:\SLDP Railroad Train Guidance System\Commissioning Test.vi
on the PC connected to the train layout. Your TA will test your VI by running your program with various combinations of tracks being blocked.
Important: If you are having difficulties completing the requirements for Benchmark Assessment B, please go to Open Lab sessions and ask for help, or otherwise get in touch with your lab TAs, recitation TAs, or come to the TA office in RH515A.
Milestone 3
Look ahead: What tasks are planned between now and the completion of the project?
See How To Give a Milestone Presentation for the format of a Milestone presentation.
Milestone 3 Deliverables:
- Presentation:
- Project description
- Design approach
- Design changes since Milestone 2
- Mission statement
- Updates to logic design
- Truth tables
- Karnaugh maps
- Boolean equations
- VI interface
- Cost estimate (previous and current). What changes were made?
- MS Project schedule (previous and current). What changes were made?
- Progress update: current state of the project (time, budget, etc.)
Commissioning
Refer to the syllabus for the commissioning deadline. There are penalties for not completing on time. Refer to the EG1003 Grading Policy for more information.
Load your VI into the PC connected to the train layout, and interface it with the Commissioning Test VI. The Commissioning Test VI can be located at
C:\SLDP Railroad Train Guidance System\Commissioning Test.vi
Finally, your TA will test your VI such that it indicates no path correctly. If your VI completes all tests successfully, you will be commissioned.
Final Presentation
The Final Presentation will be a technical briefing, similar to the Milestones, but also serves as a sales presentation explaining why your company should be selected instead of the competition.
Your Final Presentation must include:
- Company profile
- Company name
- Employee profile, role(s), and qualifications
- Mission statement
- Problem statement
- Why is the project happening?
- What does the audience need to know?
- Project objective
- What is the purpose of your project?
- Who does your project help?
- What problem does your project solve?
- Project description
- Specify LEED certification
- Examples of LEED implementations in Revit
- Revit drawings
- All floor plan drawings
- Dimensions
- 1:240 scale
- Views of exterior of building: front elevation, side elevation, isometric elevation
- Dimensions
- Specify LEED certification
- Market and product viability
- Does your company have competitors?
- What makes your project unique?
- How does your design compare to competitors - cost, quality, features?
- Is the project versatile?
- What is the price of your project?
- Conclusion
- Reiterating project purpose
- Highlight project features
- Future goals of the company
- Why should your company be awarded this contract?
- Video pitch
- Price of project
- Walkthrough animation of building in Revit
- Embedded into Final Presentation
- A description of the problem
- An overview of your solution
- A description of your company and why it is qualified to successfully do this job
- A sample of the truth tables you created
- The resulting logic equations derived and simplified via your K-Map
- Your final LabVIEW programs
- The cost estimate
- Your MS Project from each milestone showing your progress
- A video of the locomotive traversing the layout from left to right and returning
- Why your company is the best choice in awarding this contract
Submission
All SLDPs must be submitted online. Please visit this page for the link to the Project Submission form and each project’s individualized login information. To submit, login to the EG1004 website using this special login information. Submitting with an NYU account or any other account will generate an error. Components may be resubmitted at any time before the deadline. Please note that submission times are based on the most recent submission.
Please note the deliverables for this project are as follows. If any of the following items are omitted, there will be a penalty. Be sure to click "Submit" at the bottom of the form and allow sufficient time for uploading. The following list includes deliverable items that are required:
- Submission deliverables:
- Final presentation
- Cover page and table of contents
- Truth tables
- K-maps
- Simplified Boolean equations
- LabVIEW VI
- Video
- Final MS Project Schedule
- Final cost estimate
- Resume(s) (No fictitious resumes will be accepted.)
Early Submission
If the project is submitted one academic week early (before the end of the lab period the week before the Final Submission deadline), the project is eligible for a bonus that will be added to the final SLDP grade. All deliverables must be submitted one academic week before the submission deadline (see syllabus for the exact date). The deliverables received early are the ones that will be used in the Final Presentation. No changes to the submitted deliverables will be accepted.
Late Submission
Late submission is not allowed. If a project does not Commission or receive Partial Commission by the deadline set forth in the syllabus, the project will not be allowed to submit and will receive a 0 for the project grade. To receive Partial Commissioning, two TAs must evaluate the project and determine its degree of completion according to the Commissioning requirements and the project will be given a grade accordingly. Please refer to the EG1004 Grading Policy for more information.
Appendix A: Train Electrical Specifications
Output control of the track
Each part of the track is separated into different sectors. The sectors can be classified into two types, X and Y (refer to the diagram). Sectors 1, 3, 5, and 7 are X type and Sectors 2, 4, 6, and 8 are Y type.
There is a Sub-VI that will be provided that will cause the tracks to move depending upon which data is sent to the VI. Only include this Sub-VI in your their logic VI. The Sub-VI has eight inputs which are Boolean named, Sector 1 through Sector 8.
For the X type sectors, a Boolean value of True will cause the tracks to be oriented for the train to cross. A Boolean Value of False will cause tracks to be oriented for the train to go straight.
For the Y type sectors, a Boolean value of True will cause the tracks to be oriented for the train to be diverted to the diagonal track. A Boolean value of False will cause the tracks to be oriented for the train to travel on the straight track.
Input from the track
Appendix B: LabVIEW
Note: The following instructions are for your VI that will interface with the Benchmark Assessment A, as well as the Commissioning VI.
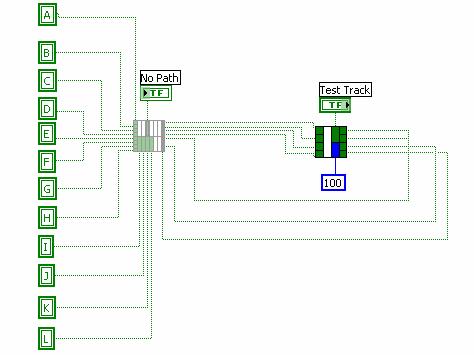
On the front panel, there must be 12 Boolean switches to represent the 12 inputs of the train, a menu ring to indicate the train's starting position (top, middle bottom), a Boolean switch to indicate whether the train is operating in Normal Mode or Reverse Running Mode, eight Boolean lights to represent each of the eight sectors, and one Boolean light to represent No Path. For Benchmark Assessment A, you will have fewer available Boolean switches and Boolean lights, so only fill in or set the ones that are present on your VI.
- On the front panel of the LabVIEW program, right click on the connector icon on the top right hand corner icon. Choose Show Connector.
- Right click on the connector icon and select Patterns. Choose the pattern with 28 nodes.
Front Panel Object Definitions
When creating your VI, please adhere to the following definitions for the inputs and outputs of your front panel objects. Failure to do so will result in your VI not working as intended when it comes time to commision on the physical track.
| True | False | |
|---|---|---|
| Blocking Signals A through K | blocked | not blocked |
| Direction of Travel | right-to-left | left-to-right |
| Travel Mode | Reverse Running Mode | Normal Mode |
| Sectors 1 through 8 | cross | straight |
| No Path | no path | path exists |
- To assign the Boolean switches and displays to a node, click on the Boolean switch or light on the front panel then click on the node you wish to assign it to.
- If you make an error in a connection, right click the incorrect terminal and select Disconnect This Terminal.
- The 8 nodes on the left side will be for the Boolean switches representing inputs showing occupancy for locations A-H. The 4 nodes on the bottom half of the icon starting from the left will be the inputs for locations I-L.
- Connect the 8 Boolean outputs that represent the orientation of the sector to the 8 nodes on the right side of the icon.
| Input A |
No Path |
Direction of Travel |
Top or Bottom |
Reverse Running Mode |
Sector 1 | ||
| Input B |
Sector 2 | ||||||
| Input C |
Sector 3 | ||||||
| Input D |
Sector 4 | ||||||
| Input E |
Input I |
Input J |
Input K |
Input L |
Sector 5 | ||
| Input F |
Sector 6 | ||||||
| Input G |
Sector 7 | ||||||
| Input H |
Sector 8 |
- Replace the faded icon in the program Commissioning Test.vi with your digital logic VI. Right click on the icon and choose replace. Then choose Select a VI and find your VI. Replace it as shown in Figure 3.
- Before testing your digital logic circuit, turn on the power to the middle workbench where the two power supplies are connected.
- Continuously run the Commissioning Test.vi and ensure that the lights on the front panel accurately represent the presence or absence of a train.
- Flip the Reset switch up and down and the track will be preset to the specified orientation.
- Once those parameters are checked, test the digital logic circuit by flipping the Test Track switch.
Appendix C: Drop Down Selection Box
In order to create and use a drop down selection box in your project, please closely read the following instructions that will aid you in creating and configuring the drop down box for use in your project:
- The very first step in the entire drop down box creation process is placing the to-be configured drop down control on the front panel of your VI. Go ahead and right-click anywhere on the front panel; select Text Ctrls, followed by Menu Ring. You should now see a drop-down menu appear on the front panel, which should look similar to the following:
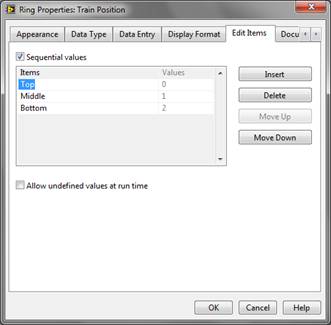
- Next, we will need to add some appropriate selections to the drop-down box you created in the last step. These selections will facilitate multiple modes of the drop-down box and therefore let you control many different cases of one control structure. Right-click on your drop-down menu on the front panel, and click Edit Items. You should see a dialog box appear on the screen. Click on the insert button, and enter the name you will assign the TOP track. Hit the return key and enter the name you will assign the MIDDLE track. Repeat this process again for the BOTTOM track. After entering the bottom track, check to make sure that there are exactly three items entered. Your screen should look like the following: Hit OK and your drop-down menu will have the correct settings to implement your digital logic.
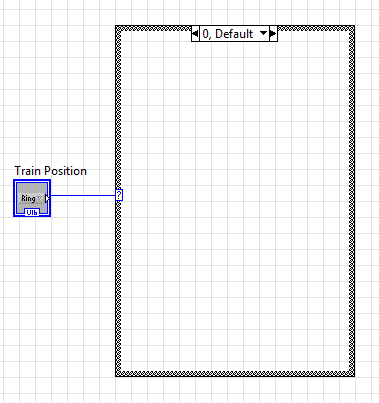
- Finally, we want to use the drop-down menu to control a case structure. Create a case structure on the back panel and wire the drop-down menu to it. You will notice that there are currently only two different cases available in the case structure. We do not want this, as there are three different positions that the train can be placed on. Right click on the case structure and select Add Case After. This will create a third case, which is necessary for completing the digital logic for the train. You will notice that the three different cases are labeled 0, 1, and 2. Case 0 refers to the top track, case 1 the middle track, and case 2 the bottom track. Do NOT change these labels to any text, your VI will not function if you do this. Your back panel will look similar to the following:
Appendix D: Boolean Logic
It is important to have a solid foundation in Boolean Logic when designing the RTGS system. The technique that is recommended for approaching this project is to create truth tables, generate Kaurnaugh maps (K-maps), generate logical equations, and simplify those equations. These simplified equations can be implemented using gates in the LabVIEW software. This guide presents a standard method for using this technique, it is highly recommended to read this entire section before beginning the project.
Truth Tables
A truth table is a chart which shows what happens under any circumstance for a logical device. Any logical system, that is a system which has binary (0’s and 1’s) input can be considered a finite state machine. This means that all the possible combinations of inputs can be known, and all the possible outcomes of those inputs can be plotted. The number of combinations of inputs can be determined by the number of input variables:
Thus when we have 5 possible obstructions on the track, which can either be on or off, we have 25 possible combinations of those obstructions, which in this case is 32. This number tells you how many rows you must put in your truth table.
When you begin writing your truth table, always start by writing all the input combinations. It is simple to calculate how many there should be, but to ensure each possible combination is included with no repeats, follow this procedure:
- We have an example logical system with 3 variables, thus there are 8 possible combinations of these 3 variables that we can have
- Each variable gets its own column in the table, in whatever order you like, as long as you keep track of it
- Starting with the rightmost column of inputs, write “0” in the first row of the table, then “1” in the next row, then “0”, then “1”, and so on, alternating the value of the column every row
- In the next column to the left, write “0” in the first two rows, then “1” in the next two rows, alternating the value every two rows
- In the leftmost column of our example table, write “0” for the first four rows, then “1” for the last four rows
- For systems with a greater number of variables, continue the pattern, doubling the number of rows before you alternate the value in each successive column
| A | B | C |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
| 1 | 1 | 1 |
Here is what the truth table should look like, with 0s and 1s colored differently to show the pattern:
Note that this truth table only shows the inputs. The outputs have not been written in yet. They will occupy their own columns. When you design the RTGS logic, each obstacle will be an input column, and each switch will be an output column. When you are figuring out the logic of the RTGS, remember that it is very difficult to approach the system as a whole.
Keep in mind what are some ways to approach the problem using Boolean logic? Which do not require a giant truth table?
Karnaugh Maps
A Karnaugh map (K-map) is a diagram that aids the visualization of something called prime implicants. The term itself is less important and can be explained implicitly through the charts themselves. Essentially, we create K-maps to help see the simplified Boolean equation of a system directly without needing Boolean algebra. However, the K-map method is limited to systems with at most four variables. With five-variable or greater K-maps can get very complicated.
When we draw a K-map, variables are grouped geometrically rather than in separate rows. Let’s begin with the simplest example, a 2-variable K-map. Our map takes the shape of a 2x2 square table, with variable “A” over the right two squares and variable “B” over the bottom two squares:
| 0 | 1 | ||
|---|---|---|---|
| 0 | 0 | 1 | |
| 1 | 1 | 1 |
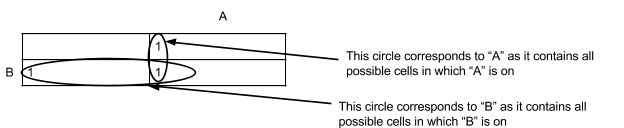
The above Karnaugh Map shows the logic for the Boolean OR operation. The cells that the variable is superimposed over correspond to input rows from the truth table for when that variable is 1. In other words, variable “A” has a value of 1 when the input combination AB is 10 or 11. In the truth table for OR, 10 and 11 both output a value of 1. Thus both cells underneath “A” are marked with a 1. Likewise, “B” has a value of 1 when AB is 01 or 11. Both these combinations in the truth table have an output of 1 as well, so we mark the cells with a 1, noting that marking the cell corresponding to 11 is redundant. The top left cell, which corresponds to 00, has 0 as its output, so we do not mark the cell.
You can think of the cells that are “covered” by each variable in the K-map as being the cells that correspond to when a variable or obstacle is “on”. The cells that are not covered are the input combinations for when that variable is “off”. The cells themselves each correspond to one output from the truth table. A K-map can only be made for one output variable at a time.
To obtain our Simplified Boolean Equation, we must circle groups of 1’s in our K-map and correlate them to logical statements. We can only circle adjacent 1’s and only in powers of two. Working with the K-map from above, we can circle the rightmost two 1’s and we can also circle the bottom two 1’s. In general, you should avoid circling the same cell more than once, however to generate maximum-sized circles, it is sometimes unavoidable. Now that we have our circles, we may now write the logical expression they represent:
Each individual circle is added to obtain the final Boolean equation. Thus, in our example, the circles add to make the statement A+B. Our Boolean equation is OUTPUT = A+B, which is simply the OR gate.
Boolean Algebra
In general, it is easier to use the K-map to simplify truth tables that are relatively small (less than five variables). However, you may find the need obtain simplified expressions logical systems of a large number of variables, which requires Boolean algebra. In general, an unsimplified Boolean equation obtained directly from the truth table will contain one term for each 1 (maxterm) in the output variable. One equation can only define one output variable at a time. Let’s look at an example truth table of three input variables. We are primarily interested in the output column, which is highlighted in red. The output column values are arbitrary, we are trying to determine their logic:
| a | b | c | out |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
So we see that the output, out has a value of 1 when abc, in order, are 001, 011, 101, 110, or 111. Writing these in terms of variables (1 corresponds to a, 0 corresponds to or any other variable), we get:
Boolean algebra is the process that helps us simplify our Boolean equation. Using a few rules, we can get the same “simplest” expression as we would with a K-map. There are many more rules to Boolean algebra, here is an abbreviated list:
- Substitution: Any variable listed in these rules may be substituted for a larger expression. e.g, let
- Identity: and
- Distributive property of addition:
- Distributive property of multiplication:
- Cancellation property: and
- Another type of identity: and
- Another type of cancellation: and
- Repeated variables: and
- Double inversion:
- Associative property of addition:
- Associative property of multiplication:
- Redundancy: and
- NAND and NOR principle: and
- One useful simplification: and
- Order of Operations: PNAO: Parentheses, NOT, AND, OR
One of the first simplifications that can be made to the equation above is to factor out c from the first three terms and the last one. Like in regular algebra, Boolean variables can be factored when they share the same value across multiple terms. [Rule 3] We now have:
In fact, we can factor the expression within the parentheses even further:
Look at the statement within the inner parentheses. When we read out the first and last terms, the statement is true whether b is false or true. [Rule 5] Thus we may rewrite as 1, and the whole statement in the brackets becomes:
.
When any variable is in an AND statement with 1, it becomes just the variable alone. [Rule 2] The result solely depends on the variable.
.
Again, we apply Rule 5 on a to get . Rule 2 can be applied again.
The statement is close to completely simplified, but there is still one more step. In the second term, there is a multiplied with ab. This is superfluous because the term c is already in our expression. In other words, any combination involving c has already been accounted for, thus the remaining terms in the equation will work independently of c. [Rule 12] Our simplified Boolean equation is:
Note that terms are independent of the order of their arguments, meaning that we can rearrange variables in an equation and still mean the same thing. [Commutative property]
In the RTGS project, each blocking signal acts as an input variable, and each sector switch acts as an output. Obtaining the simplest Boolean equation will be important to streamline any troubleshooting later and to implement the logic in LabVIEW in the simplest manner possible.




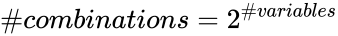
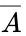
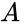
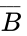
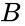
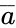 or any other variable), we get:
or any other variable), we get:
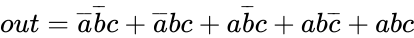
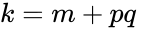
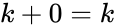 and
and 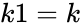
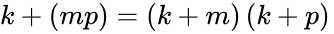
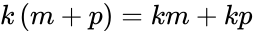
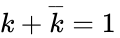 and
and 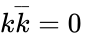
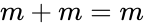 and
and 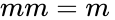
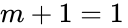 and
and 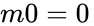
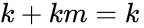 and
and 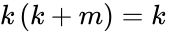
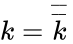
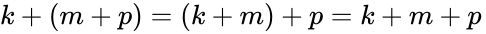
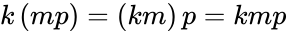
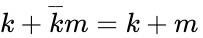 and
and 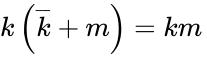
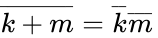 and
and 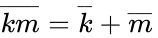
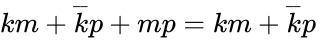 and
and 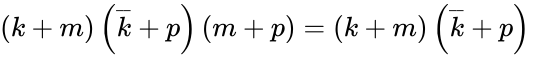
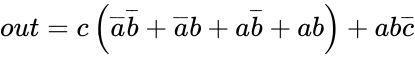
![{\displaystyle out=c\left[{\overline {a}}\left({\overline {b}}+b\right)+a\left({\overline {b}}+b\right)\right]+ab{\overline {c}}}](https://wikimedia.org/api/rest_v1/media/math/render/png/033c5617b9c3563fd55052ba21b3fce8ca39eac6)
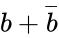 as 1, and the whole statement in the brackets becomes:
as 1, and the whole statement in the brackets becomes:
![{\displaystyle out=c\left[{\overline {a}}1+a1\right]+ab{\overline {c}}}](https://wikimedia.org/api/rest_v1/media/math/render/png/dc19a6c305f350eb0220690f347079cbca116d47) .
.
![{\displaystyle out=c\left[{\overline {a}}+a\right]+ab{\overline {c}}}](https://wikimedia.org/api/rest_v1/media/math/render/png/8a9dfa129e37f434a929438553b996f107041cae) .
.
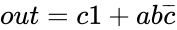 . Rule 2 can be applied again.
. Rule 2 can be applied again.
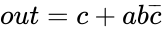
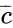 multiplied with ab. This
multiplied with ab. This