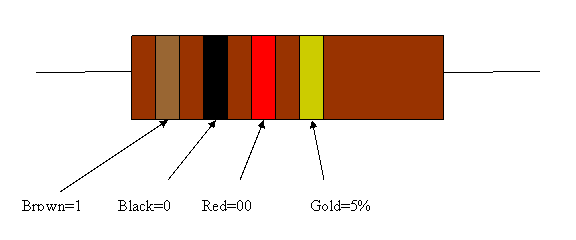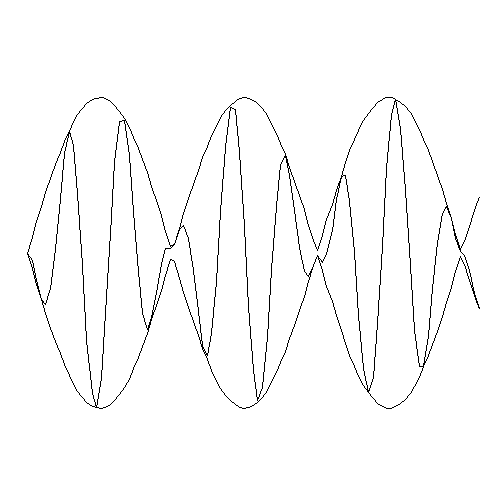Difference between revisions of "Electronic Filters"
| Line 33: | Line 33: | ||
This is why when a trumpet and clarinet both play the same musical note they | This is why when a trumpet and clarinet both play the same musical note they | ||
sound different — their harmonics are different. We hear the base frequency | sound different — their harmonics are different. We hear the base frequency | ||
plus the harmonics of these instruments. Rock guitars | plus the harmonics of these instruments. Rock guitars have their distinctive | ||
sound by adding harmonics to the note they play.</p> | |||
<embed | <p><embed><drc=guitar.mp3></embed></p> | ||
<p>Radio waves work differently than | <p>Radio waves work differently than | ||
Revision as of 03:26, 16 December 2006
EG1004 Lab 10: Electronic Filters
1 OBJECTIVES
The experimental objective of this lab is to build two electrical circuits and to test them using a virtual bench oscilloscope in order to identify each as a low-pass, or high-pass, or band-pass filter. The -3dB point for each filter will also be identified. Finally, we'll build a simple radio that doesn't require a battery to operate as an example of a band-pass filter.
Together, we will learn how electrical filters are used, how resistors, capacitors, and inductors function in a filter and the significance of the -3dB point.
2 OVERVIEW
It is important for electrical engineers to be able to selectively filter certain frequencies. An electrical filter works by allowing only designated frequencies to pass through. By tuning your radio to a particular station, you are isolating a certain frequency. The filter selects the station you have chosen from the hundreds of different stations that are broadcasting. How does the filter accomplish this?
To understand how filters work, we need to identify the elements that make electrical filtering possible. Signals that occur naturally are composed of many frequencies.
For example, the human voice is composed of frequencies ranging from 0–4kHz. A signal consists of a primary frequency, called a base frequency, plus additional multiples of that frequency with different loudness called harmonics. Different devices will have different harmonics. This is why when a trumpet and clarinet both play the same musical note they sound different — their harmonics are different. We hear the base frequency plus the harmonics of these instruments. Rock guitars have their distinctive sound by adding harmonics to the note they play.
<embed><drc=guitar.mp3></embed>
Radio waves work differently than sound waves. The signal has a base frequency, and the information we hear is contained in adjacent frequencies called sidebands.
Voltage, or electromotive force, and frequency are the building blocks of an electrical signal. Voltage is a force that propels electrons through a medium. Current is the amount of electric charge flowing past a specified circuit point per unit time. Frequency is the rate at which the signal repeats itself. The gain of a circuit is the ratio of its power compared to its input. For devices that do not produce energy, such as this lab, the gain cannot exceed one. However for devices such as transistors and other amplifiers, the gain can be much greater than one.
A filter is a circuit that shapes and controls the bandwidth of a signal; bandwidth is the range of frequencies that the filter allows to pass. For example, when we turn up the bass of an audio amplifier, we are using a filter that passes the low frequencies more than the high frequencies. Also, when we tune a radio, we are using a filter that allows the base frequency plus the sidebands of the desired station to pass, but not other stations.
The filters that we are going to build are composed of resistors and capacitors. A resistor resists the flow of electrons by converting some of the electric energy to heat. The voltage across a resistor obeys Ohm's Law: V = IR, where I is the current and R is the resistance. Varying the frequency of the voltage will not affect the voltage across the resistor.
A resistor is designed to impede the flow of electricity and dissipate electrical energy in the form of heat. Resistors work by having the electricity flow through a poor conductor such as carbon. The unit of resistance is the Ohm, named after Georg Ohm, and is represented by the capital Greek letter Omega (“Ω�?).
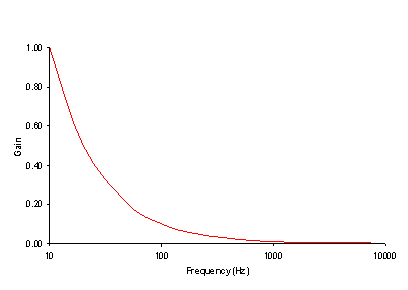
Capacitors are metal plates that are separated from each other, allowing electric charge to accumulate on the plates. These plates store energy rather than dissipate it, like a resistor. For DC voltage, provided by a device like a battery, the plates will gather charge, and once the plates are charged, will no longer pass current, so the capacitor looks like an “open circuit�?, where nothing is connected. For high frequencies, the charge can quickly gather and dissipate off the plates, allowing current to flow through the capacitor freely, making the capacitor behave like a “short circuit�?. The unit of capacitance is the Farad, named after Michael Faraday, and is represented by the capital letter “F�?. The relationship between the voltage across a capacitor and varying frequencies is shown in Figure 1.
Figure 1: Capacitor frequency response
Inductors, also known as coils or chokes, are coils of wire that allow the current through the wire to form a magnetic field. Like capacitors, inductors store energy, but in the magnetic field instead of on plates, and its behavior is the opposite of a capacitor. For DC voltage, the current will make a stable magnetic field and the current will flow freely, making the inductor look like a “short circuit�?. At high frequencies, the magnetic field does not have time to form before the current reverses and the field collapses, causing the inductor to resist the current flow, looking like an “open circuit�?. The unit of inductance is the Henry, named after Joseph Henry, and is represented by the capital letter “H�?. The relationship between the voltage across an inductor and varying frequencies is shown in Figure 2.
Figure 2: Inductor frequency response
The elements of filters, such as resistors, capacitors, and inductors, are connected by conductors (wires) that carry electrons between these devices. The voltage is the same throughout the entire conductor, so the voltage across the two ends of the conductor is zero.
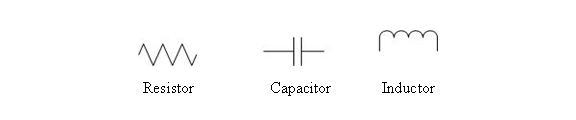
How the components are connected is shown using a schematic diagram. Each component is represented by a symbol, and the connections between components are represented by lines. The symbols are designed to represent the physical characteristics of the components. Therefore, a resistor is represented by a zigzag line showing how the electricity’s path is impaired. A capacitor is shown as two parallel lines, representing its plates. Finally, an inductor is shown as a series of looping lines, representing the coils of wire it has. The schematic diagram symbols for these components are shown in Figure 3.
Figure 3: Component schematic symbols
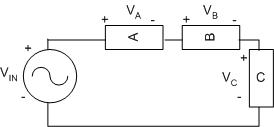
Different combinations of resistors and capacitors allow engineers to build different kinds of filters to perform specific tasks. Resistors, inductors, and capacitors can be arranged in three different ways. In a series circuit, the element's conductors are connected end to end. The current in a series circuit remains the same in all the electrical elements. In a series circuit, as shown in Figure 4, the sum of the voltages across each element is equal to the voltage of the power source (VIN = VA + VB + VC).
Figure 4: A series circuit
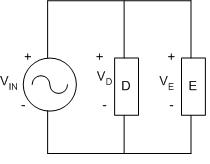
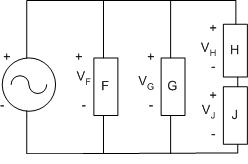
In a parallel circuit, as shown in Figure 5, the element's conductors are connected at opposing ends. The current that is supplied by the voltage source equals the current that flows though elements D and E. The voltage across the elements that are parallel is the same (VIN = VD = VE)).
Figure 5: A parallel circuit
Series and parallel circuits can be combined, as shown in Figure 6:
Figure 6: A hybrid circuit
The voltage across the top and bottom connectors is the same, so (VIN = VF = VG = (VH + VJ)).
To produce a graphical representation of the characteristic behavior of the circuit being analyzed, it is necessary to graph the gain of the circuit versus the frequency of the electrical signal. Gain is a measure of the power produced by the circuit, measured in decibels, and is calculated using the following formula:
A 3dB drop of signal power is the point at which the signal power is half of its original value. The frequency corresponding to this -3dB point is also called the cutoff frequency of the filter. Note that since the filters we are using only contain passive components, the output cannot be larger than the input. Therefore, the gain will always be a negative number because we are taking the logarithm of a number less than one.
If you examine the preceding formula, you’ll see that for the gain to be -3dB, VOUT must be VIN divided by the square root of 2 (1.414), more easily written as VOUT=VIN/1.414. Therefore, the -3dB point of a circuit is the frequency that causes the output voltage to be .707 times the input voltage.
Types of Filters
Your job, once you have built the electrical filters according to the specifications in this manual, is to identify them. In order to do this, we must define the three possibilities.
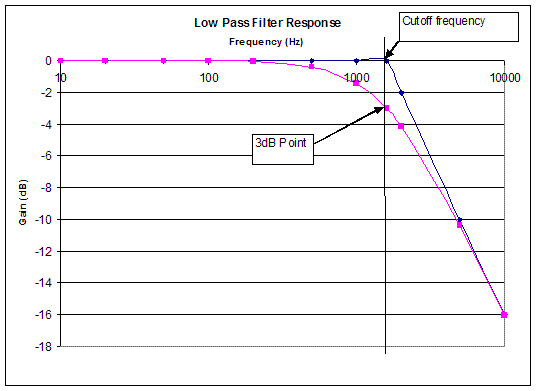
Sometimes, it is beneficial to remove the high frequency components from a signal because this is where unwanted noise frequently exists. To do this, a low-pass filter is used. It passes the low frequencies while blocking the higher ones. The low-pass filter shown here has a gain that drops from 0dB to -3dB at 1590 Hz, which is its -3dB point and corresponding cut-off frequency. Thus, the filter has a bandwidth of 1590Hz and it only allows frequencies from 0Hz to 1590Hz to pass through at full power. Figure 7 shows the characteristic behavior of a low-pass filter. A trend line showing the response of the filter is also shown. Note that for low frequencies, the gain is 0dB, meaning that the output equals the input. The filter suppresses high frequencies, as shown by the trend line on the right. The intersection of these two trend lines will be at the cutoff frequency, giving another reason why the cutoff frequency is important.
Figure 7: Characteristic behavior of a low-pass filter
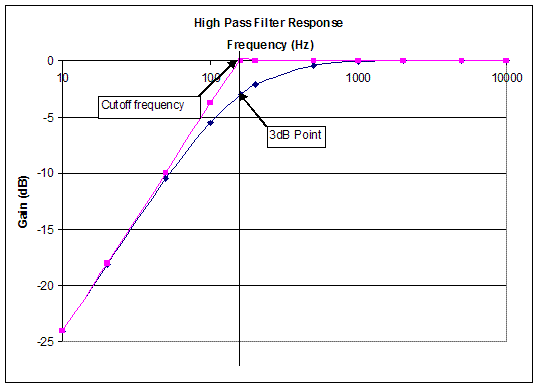
A high-pass filter passes the high frequencies but blocks the low ones, the opposite response of a low-pass filter. The -3dB point for this filter is 160 Hz. This is determined using the same method we used for the low-pass filter. Thus, we can say that the filter has a bandwidth of 60 Hz to infinity and that the filter only allows frequencies greater than 160 Hz to pass through. Figure 8 shows the characteristic behavior of a high-pass filter as well as the trend lines and their intersection at the cutoff frequency.
Figure 8: Characteristic behavior of a high-pass filter
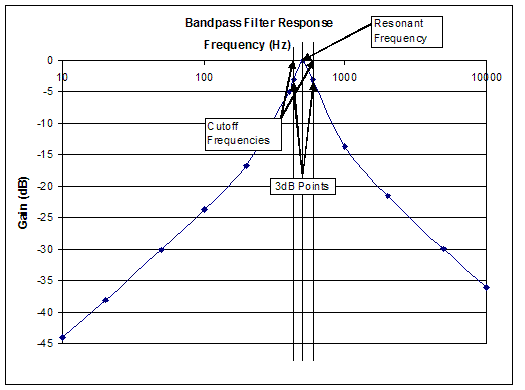
A band-pass filter only allows a certain range of frequencies to pass through and blocks all other frequencies. The frequency of the highest response point is called the resonant frequency, and for an ideal filter will be 0dB. This type of filter has two -3dB points, one above the resonant frequency and one below it, and therefore two cutoff frequencies. The difference in these two cutoff frequencies is called the bandwidth of the band-pass filter. Figure 9 shows the characteristic behavior of a band-pass filter.
Figure 9: Characteristic behavior of a band-pass filter
The band-pass filter shown here has a resonant frequency of approximately 500Hz, and has -3dB points with cutoff frequencies of approximately 400Hz and 600Hz. Therefore, the bandwidth of this filter is approximately 600Hz-400Hz, or 200Hz.
Finally, a notch filter rejects a specific range of frequencies and passes the others. Looking at it another way, a notch filter is the exact opposite of a bandpass filter. Notch filters are frequently used to remove interference from a desired signal.
Note: the filters here are "ideal" filters, and show total power transfer (0dB) at their maximum response. Real filters frequently show some losses, and may have a maximum response less than 0dB. However, the -3dB point is still defined according to the formula shown above.
Now, we are ready to build the circuits that will produce the electronic filters. Before we start, it is important to understand the breadboard we will be using to connect the elements of our circuits. Breadboards have horizontal and vertical connectors. The front of the breadboard is shown in Figure 10a. The back of the breadboard, with its protective cover removed so you can see the internal connections, is shown in Figure 10b.
Figure 10a: Front of Breadboard
(Red squares indicate where connections are broken, making two indepdent halves)
Figure 10b: Back of Breadboard
(Red squares indicate where connections are broken, making two indepdent halves)
Finally, you'll need to identify the resistors and the capacitors required to complete your circuit. To identify the resistors, you must look at the colored bands. Hold the resistor horizontally with the three bands that are close together to the left, as shown in Figure 11. The first two colors determine the first two digits of the resistance, and the third band determines how many zeroes to add. Each colored band represents a particular number.
Figure 11: Color-coded bands on a 1kΩ resistor
Resistor color code:
| Color | First Band | Second Band | Third Band |
| Black | 0 | 0 | X1 |
| Brown | 1 | 1 | X10 |
| Red | 2 | 2 | X100 |
| Orange | 3 | 3 | X1000 |
| Yellow | 4 | 4 | X10000 |
| Green | 5 | 5 | X100000 |
| Blue | 6 | 6 | X106 |
| Violet | 7 | 7 | X107 |
| Gray | 8 | 8 | X108 |
| White | 9 | 9 | X109 |
The fourth band indicates a tolerance of the resistor, which means how close its actual resistance will be to the value indicated by the bands:
| Color | Tolerance |
| Gold | 5% |
| Silver | 10% |
| No band | 20% |
As an example, a 470kΩ resistor with a 5% tolerance would have color bands of yellow, violet, yellow, and gold. You should check this yourself to be sure you know how to read the colors.
For capacitors, the value is stamped on the capacitor, especially if the capacitor is large. Most capacitors have very small values. For small capacitors, the most common ranges are microfarads (shown as µF), nanofarads (shown as nF), and picofarads (shown as pF). The following conversion table may help you understand how these ranges relate to each other:
1 µF=103nF=106F
1 nF=103pF
Sometimes the value is coded. The following rules are commonly used in marking
values on capacitors:
- If there are only two digits on the capacitor, the value is in picofarads (nF)
- For three digits, the first two digits of the number are the overall value of the capacitor, and
the third is a power of 10, with the overall value being in picofarads. For example, a capacitor with a
value of 103 would be 10*103 picofarards, or .01 nanofarads. To make this a little easier, the
table might be helpful:
CODE/Marking µF
microfaradsnF
nanofaradspF
picofarads100 0.00001 0.01 10 101 0.0001 0.1 100 102 0.001 1 1000 103 0.01 10 10000 104 0.1 100 100000 105 1 1,000 106 106 10 10,000 107 107 100 100000 108 - Finally, capacitors might use a series of colored bands, like resistors, with exactly the same meaning, except the units are in picofarads instead of ohms.
Also, where there are digits on the capacitor, there might be a letter following the digits. This indicates the tolerance of the capacitor according to the following table:
| C | +/-0.25pF |
| D | +/-0.5pF |
| F | 1% |
| G | 2% |
| J | 5% |
| K | 10% |
| M | 20% |
| Z | +80-20% |
The following figures show two capacitors. You can use the preceding tables to verify their values.
.001 µF Capacitors |
.01 µF Capacitors |
For inductors, the value is stamped on the inductor. If you can’t find the value, ask your TA for help.
3 YOUR ASSIGNMENT
Individual Lab Report
Follow the lab report guidelines laid out in the page called Specifications for Writing Your Lab Reports in the Technical Communication section of this manual. As you write, the following discussion points should be addressed in the appropriate section of your lab report:
- What is an oscilloscope? You may have to do some research to answer this question.
- Observe the graphs generated from each circuit. What type of filter does each circuit produce?
- Does each circuit produce the expected result? If not, explain why.
- Locate the -3dB point on each graph and cutoff frequency to determine the bandwidth of each filter.
- What is the -3dB point used for?
- Name at least one object that uses each type of filter.
- Discuss any problems encountered.
Team PowerPoint Presentation
Follow the presentation guidelines laid out in the page called EG1004 Lab Presentation Format in the Introduction to Technical Presentations section of this manual. When you are preparing your presentation, consider the following points:
- Discuss your findings
- Discuss the role of filters in the future
4 MATERIALS AND EQUIPMENT
- 2 100kΩ Resistors
- 1MΩ Resistor
- 0.001µF Capacitor
- 0.01µF Capacitor
- Function Generator with Cable
- Breadboard
- DAC Board
- 1N34 diode
- high impedance headphone
- 10pF capacitor
- 1mH inductor
- Appropriate Wiring
Remember: You are required to take notes. Experimental details are easily forgotten unless written down. EG Standard Note Paper can be downloaded and printed from the EG website the EG1004 Web site. Use your lab notes to write the Procedure section of your lab report. At the end of each lab your TA will scan your lab notes and upload them to the EG1004 course section on MyPoly. You must attach your lab notes at the end of your lab report (use the "Insert Object" command in MS Word after your Conclusion). Keeping careful notes is an essential component of all scientific practice.
5 PROCEDURE
Circuit Testing
- Click “Start�?, then �?Lab Menu�?, and select “Lab 10�? off the pull down menu. From there, select “Virtual Bench�?. This will open the Virtual Bench window. Select the first icon, which is “Virtual Bench Scope�?. Make the oscilloscope full screen so that it’s easy to read.
- Plug in the function generator.
- Connect the function generator to the DAC board. Each lab PC has a DAC board connected to it by a ribbon cable. Make sure your green DAC board is connected to the analog ribbon cable. Insert the coaxial end of the connecting cable into the 50Ω output on the function generator.
- The DAC board has two wires attached to pins 3 and 4. Connect the red alligator clip of the connecting cable to the other end of the pin 3 wire and connect the black alligator clip of the connecting cable to the other end of the pin 4 wire.
- Turn on the function generator using the green button. Set the range on the function generator to 1kHz. Set the function mode to Sine Wave (~ - the rightmost button of the group of three on the right top side of the function generator). Tune the output frequency to exactly 1kHz by adjusting first the Coarse and then the Fine knobs until the display reads 1.000kHz.
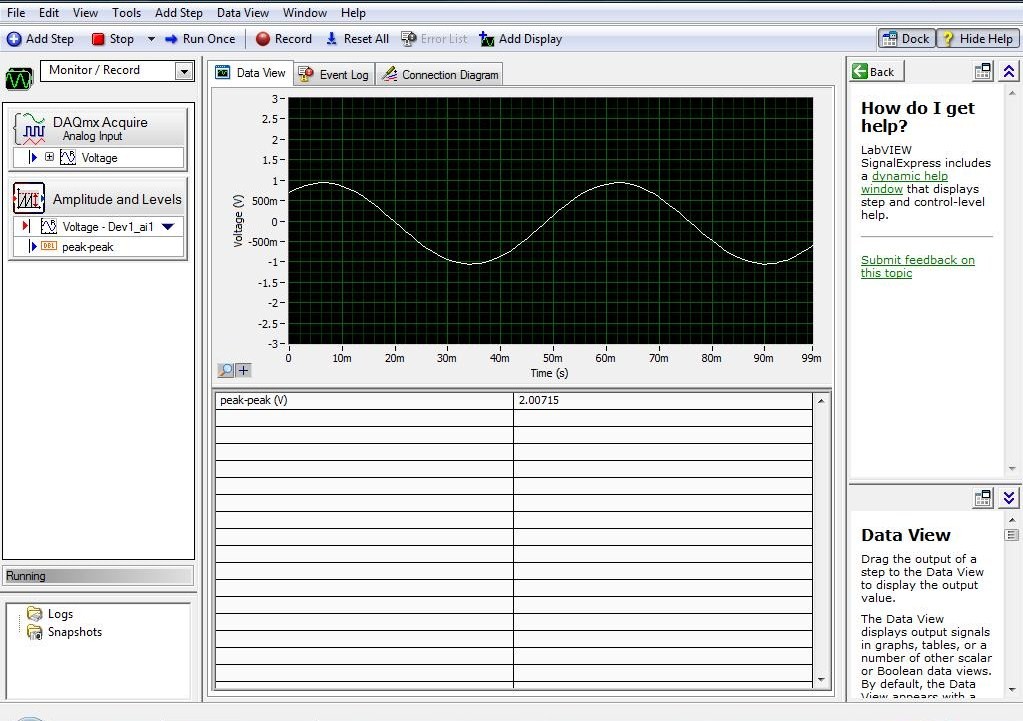
- On your lab PC, with the Virtual Bench Oscilloscope open, click Auto Setup. It will look like Figure 12.
- On the function generator, push in the Duty knob and set to zero. Pull out the Amplitude knob and set it to its maximum value. A sine wave will appear on the oscilloscope, and the peak to peak voltage will show in the bottom row of the oscilloscope next to the caption Vp-p. If Vp-p is not present, Check the "Measure" icon on the extreme right side of the oscilloscope. It should say "Ch1". If it does not, click the up arrow or down arrow until this title appears. If, after doing this, the Vp-p still doesn't appear, click on "Edit" off the main menu at the top of the screen, and click "Scope Settings". On the window that appears, make sure the following boxes are checked, and click on them to check them if they are not: Vdc, Vac, Vmax, Vmin, and Vp-p. After you've done this, click "Apply" and "OK". Vp-p should not be present on the screen. Adjust the amplitude knob until the peak to peak voltage is approximately 2.0V. If you can’t see the sine wave, click “Auto Setup�? again.
- When you have finished calibrating the function generator and the Virtual Bench Oscilloscope software, the Volts peak to peak (Vp-p) reading on your lab PC will be approximately 2.00V. Record the Vp-p reading. This is your VIN. Use this figure for all your computations. Also, calculate .707*VIN and write it down. This is your -3dB point voltage for finding the cutoff frequency.
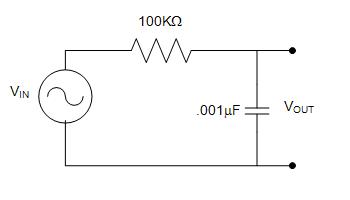
- Now we will build Circuit 1. Shut off the function generator and disconnect the alligator clips from the DAC board. Use the schematic diagram in Figure 13 to build your circuit.
- Insert each end of a 100kΩ resistor into the breadboard horizontally (long direction).
- Insert the 0.001µF capacitor into the breadboard vertically. Make sure that one of the two capacitor leads is inserted into the breadboard in the same column as one of the two leads of your resistor.
- Insert the second lead of your capacitor vertically in any pin in rows F-J.
- Now you will insert two wires into the breadboard to connect your circuit to the Virtual Bench Oscilloscope software (via the DAC board). To do this, connect the wire of pin 3 of your DAC board to the breadboard in the same column that your resistor and capacitor share. Insert the wire coming from pin 4 of the DAC board into the breadboard in the same column as the spare lead of your capacitor.
- Connect the red alligator clip from the function generator to left end of the resistor, i.e. the one not connected to the capacitor. Connect the black alligator clip to the bottom lead of the capacitor, i.e. the one not connected to the resistor, and that also has one of the wires connected to it from the DAC board. If you have wired your circuit successfully, the Virtual Bench Oscilloscope software will have a horizontal line across the center of the screen.
- Turn on the function generator. Change the frequency on the function generator in this pattern (10, 20, 50, 100, 200, 500, 1000, 2000, 5000, 10000Hz) and record the Vp-p reading at each frequency for a total of 10 measurements. Looking at your results, you will see voltages above and below the -3dB point voltage. Now find the- 3dB point exactly by starting with the frequency just below the -3dB point, and then increasing the frequency until you have the voltage corresponding to the -3dB point. Note the frequency and write it down. This is the cutoff frequency.
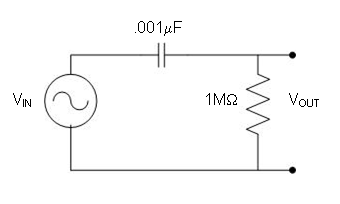
- Shut off the function generator and disconnect the all the wires, capacitors, and resistors from the breadboard. Use the schematic diagram in Figure 14 to build Circuit 2.
- Insert two wires into the breadboard to connect your circuit to the Virtual Bench Oscilloscope software (via the DAC board). Connect the wire of pin 3 of your DAC board to the breadboard in the same column that your resistor and capacitor share. Insert the wire coming from pin 4 of the DAC board into the breadboard in the same column as the spare lead of your resistor.
- Connect the red alligator clip from the function generator to left end of the capacitor, i.e. the one not connected to the resistor. Connect the black alligator clip to the bottom lead of the resistor, i.e. the one not connected to the capacitor, and that also has one of the wires connected to it from the DAC board. If you have wired your circuit successfully, the Virtual Bench Oscilloscope software will have a horizontal line across the center of the screen.
- Turn on the function generator. Change the frequency on the function generator in this pattern (10, 20, 50, 100, 200, 500, 1000, 2000, 5000, 10000Hz) and record the Vp-p reading at each frequency for a total of 10 measurements. Looking at your results, you will see voltages above and below the -3dB point voltage. Now find the -3dB point exactly by starting with the frequency just below the -3dB point, and then increasing the frequency until you have the voltage corresponding to the -3dB point. Note the frequency and write it down. This is the cutoff frequency.
- Shut off the function generator and disconnect the all the wires, capacitors, and resistors from the breadboard. Use the schematic diagram in Figure 15 to build Circuit 3.
- Crystal sets require a very long antenna and good ground, so we've made a test setup for you at the back door of Rogers Hall. Therefore, after you've assembled the rest of the radio, leave the lab and go down to the back door. At the back door you'll find the antenna, which is a long wire going up the side of the building. Connect it to your radio. Next, find the ground wire, which is a wire connected to a fire hydrant. Connect that to your radio. Next, put a plastic bag over the headphone for health reasons.
- Put the headphone in your ear, and you should hear a station. The radio is designed to hear WQEV (Radio Disney) easily.
- In your lab report and presentation, indicate how many stations your heard and, if possible, their call sign (e.g. WABC, WINS, WCBS).
- After you've operated the radio, disconnnect it from the antenna and ground, and return to the lab so you can put away the equipment and clean up your work area.
Figure 12: The Virtual Bench Oscilloscope program window
Warning: Do not touch the Amplitude or Duty knobs for rest of the lab. If you do, you will have to recalibrate both the function generator and the Virtual Bench Oscilloscope.
Figure 13: Circuit 1 (R = 100kΩ, C = 0.001µF)
Figure 14: Circuit 2 (R = 1 MΩ, C = 0.001µF).
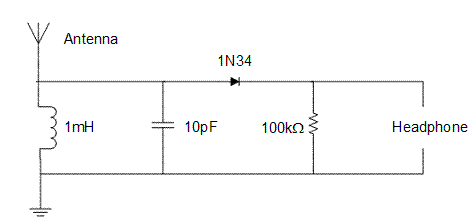
There are several items on the circuit diagram below that you might not recognize. The thing in the top left corner that looks like a rake is the antenna, and will be connected after you've completed the rest of the circuit. Similarly, the thing in the bottom left corner that has three horizontal lines is an "earth ground", which will also be connected later. Finally the thing in the top middle that looks like an arrow going into a line is called a diode. You will be given a diode as part of building your circuit. What the diode does is beyond the scope of this lab, but you'll need it.
Circuit 3 is called a "crystal set" radio. As you can see, it is an actual working radio that doesn't require a battery. It got its name because originally a galena crystal was used instead of the 1N34 diode shown in the circuit diagram. As you can see, the symbol for a diode is an arrow pointing at a line. The band-pass filter is the inductor and capacitor shown on the left side of the circuit diagram. Since this design emphasizes quick assembly using a breadboard, you'll find that the radio can only get one or two stations, but it still works. More refined design can the found on the World Wide Web via a search on the term "crystal set". A more detailed description of how the radio works is outside the scope of this lab, but a brief version is given in the Appendix below in case you are interested.
Note: The orientation of the diode is not critical to the operation of the radio - it can be put in the circuit in either orientation.
Figure 15: Circuit 3 (Crystal Set Radio)
Data Analysis
- Create two tables in Microsoft Excel (one each for the low-and high-pass filter) to record your data. Remember your VIN is a constant. Each table should look like Figure 16.
- Instruct Microsoft Excel to calculate the gain using this equation:
- Plot two Frequency (X) vs. Gain(Y) graphs using the X,Y Scatter template. Make one graph for each circuit.
- Change the x-axis to logarithmic scale. To do this, right-click on the x-axis and select Format Axis. Click on the Scale tab and check the Logarithmic Scale checkbox. Click OK.
- Identify each of the circuits as a low-, high-, or band-pass filter. If it’s a high-pass or low-pass filter, find the -3dB point and the cutoff frequency. If it's a band-pass filter, identify the two cutoff frequencies.
- For a band-pass circuit, use the graph to find the -3dB point by seeing where the curve has a value of -3dB. Compare the value from the graph to the value you actually read earlier. Are they the same?
| Frequency (Hz) | VIN (Volts) | VOUT (Volts) | Gain=20log(VOUT/VIN) (dB) |
| 10 | 2.0 | ||
| 20 | 2.0 | ||
| 50 | 2.0 | ||
| 100 | 2.0 | ||
| 200 | 2.0 | ||
| 500 | 2.0 | ||
| 1000 | 2.0 | ||
| 2000 | 2.0 | ||
| 5000 | 2.0 | ||
| 10000 | 2.0 |
Your lab work is now complete. Please clean up your workstation. Return all unused materials to your TA. Refer to section 3 Your Assignment for the instructions you need to prepare your lab report.
Appendix - How a Crystal Set Works
Note: This material is included for those who want to more about how a crystal set works. You do not have to read this section if you don't want to, and you will not be responsible for knowing this material
History
Some of the earliest radios made were crystal sets. They have a number of advantages:
- They do not require a power source such a a battery, so they can be used any time. This makes them very valuable during things like blackouts and recovery from disasters such as hurricanes.
- They have so few components they can be built quickly, usually out of whatever parts are lying around
- They are rugged because of their simplicity, so they can be used while you're traveling
- Unlike regular radios, they do not emit a signal themselves, making them excellent "stealth" radios. This is important to people like soldiers, where they can listen to the radio without giving away their position.
The radio has several major components:
- An antenna, which should be as long as possible - the longer the antenna, the more stations you'll hear.
- An earth ground. As the name implies, this connects the radio to the earth, allowing an signals it receives to return to ground to complete the circuit for the voltage the signal makes.
- A bandpass filter consisting of an inductor and a capacitor. Usually the values of one or both these components can be changed, or varied. For the inductor, if it can be varied it's by turning a rod going through the middle of the inductor. For the capacitor, if it can be varied the capacitor plates are visible, and can be rotated. Changing these values allows the allowable frequency to be changed, tuning the radio.
- A diode, shown in the middle of the circuit diagram. If you could look at the signal from the bandpass filter,
would look like a sine function (like you saw with the low-and high-pass filters), but instead of its amplitdue being
constant, it would change substantially. A typical signal is shown below:
Figure 17: Received signal waveform
The variation in the waveform is the audio signal (sound) we want to hear. This is called Amplitude Modulation, or AM for short.
A diode is a device that passes electrical current in one direction. A galena crystal can be used as a diode, which is how the crystal set got its name. However, there are many other materials that can be used as a diode as well. During World War II, many soldiers used a rusty razor blade as a diode. After the invention of semiconductors, diodes are now made of silicon or germanium. For a crystal set, germanium is a better choice. In electronics in the United States, diodes have names that start with "1N", followed by a number and possibly a letter. The number is a serial number assigned by agreement among the electronics manufacturers. A letter, if present, indicates an improved version of the product. Therefore, the diode used here is 1N34, but the improved 1N34A could be used as well. Transistors always start with the designation of "2N", with other semiconductors have designations of "3N", "4N", and so on.
The diode is used as a detector, which detects the sound from the radio wave. It does this by removing the negative part of the sine wave, leaving only positive voltages. The headphones then act as a low pass filter, seeing only the height of the sine wave rather than the voltage variations of the sine wave itself. As we said earlier, this amplitude is tha audio signal we're looking for, so we hear it.
- The headphone, which is how we hear the radio station. Sometimes a resistor is put in parallel with the headphone to boost the signal
The negative thing about crystal sets is that they are essentially a craft item. Sometimes they don't work for no apparent reason. Sometimes they work in ways we don't totally understand. Many people view this as fun, not knowing what to expect. Others view it as a source of frustration. Either way, they are always exciting.
If you want to know more about crystal sets, the easiest way to get started is to use a search engine such as Google with a criterion such as "radio crystal set".