Difference between revisions of "Boom Construction Competition"
Jbringardner (talk | contribs) |
|||
| (113 intermediate revisions by 7 users not shown) | |||
| Line 1: | Line 1: | ||
=Objective= | |||
The experimental objective of this lab is to design and assemble a boom. This is a competition lab, and the booms will be judged by a design ratio that uses boom weight, boom length, weight held, and anchor time. The highest design ratio wins the competition. | |||
the | |||
=Overview= | |||
A <b>boom</b> is used to lift and move heavy objects, often objects that are much heavier than the boom itself. Distributing the load being lifted over the length of the boom is the main problem in boom design. The design must consider the maximum load the boom will be required to lift, how high the load will be lifted, and whether the boom will be moved or remain stationary while loaded. | |||
used to | |||
itself. Distributing | |||
length of the boom is the main problem in boom design. The | |||
consider the maximum load the boom will be required to lift, how high the load | |||
will | |||
== Examples of Booms == | |||
Certain types of bridges use booms. A cantilever bridge uses two booms extending from a common base. One type of cantilever bridge is a cable-stayed bridge (Figure 1). | |||
[[Image:Lab_boom_13.png|650px|thumb|center|Figure 1: A Cable-Stayed (Cantilever) Bridge]] | |||
The Ed Koch Queensboro Bridge is a double cantilever bridge (Figure 2). It has two bases with two booms extending from each base and the cantilevers placed end to end. | |||
[[Image:lab_boom_10.jpg|frame|center|Figure 2: Ed Koch Queensboro Bridge (Double Cantilever)]] | |||
The Grand Bridge over Newtown Creek is a swing bridge, also known as a rotating bridge (Figure 3). This bridge has two booms mounted on a base that rotates. | |||
[[Image:lab_boom_11.jpg|650px|thumb|center|Figure 3: Grand Bridge (Swing Bridge)]] | |||
Figure 4 shows a bascule bridge, more commonly known as a drawbridge, where it is clear that the bridge uses a big, very flat boom. | |||
[[Image:lab_boom_12.jpg|650px|thumb|center|Figure 4: Bascule Bridge]] | |||
Not all bridges are booms. Suspension bridges use a deck that is supported by steel cables, not booms. Examples of suspension bridges are the Brooklyn Bridge, Manhattan Bridge, Verrazano-Narrows Bridge, and the George Washington Bridge. | |||
Cranes are the most common example of booms. The crane pictured in Figure 5 is a tower crane. These cranes are a fixture on construction sites around the world. A tower crane can lift a 40,000 lb load. It is attached to the ground by anchor bolts driven through a 400,000 lb concrete pad poured a few weeks before the crane is erected (Howstuffworks.com, 2003). | |||
[[Image:Tower Crane.jpg|650px|thumb|center|Figure 5: A Tower Crane (Jennings, 2015)]] | |||
== Stress and Strain == | |||
The design of a boom must consider the properties of the materials used to build the boom. The mechanical properties and deformation of solids are explained by stress and strain. When an external force is applied to a material, it changes shape (e.g. changes length and cross-section perpendicular to the length). Understanding how deformation will affect materials is a critical consideration in boom design. | |||
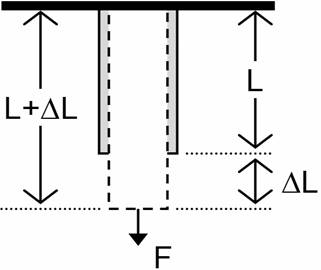
According to Serway and Beichner in “Physics for Scientists and Engineers,” <b>stress</b> is the external force acting on an object per unit cross sectional area. <b>Strain</b> is the measure of deformation resulting from an applied stress (Figure 6). | |||
deformation | |||
[[Image:lab_boom_1.jpg|frame|center|Figure 6: Material Under Tension]] | |||
Figure 6 | |||
The expression (1) for tensile stress shows the relationship between an applied force and the cross-sectional area. | |||
< | <center><math>\sigma = \frac{F}{A}\,</math></center> | ||
< | <p style="text-align:right">(1)</p> | ||
</p> | |||
In (1), σ is the stress, F is the applied force, and A is the cross-sectional area of the object perpendicular to the force. The resulting strain (2) is calculated by dividing the change in length of the object by the original length. | |||
<p> | <center><math>\varepsilon = \frac{\Delta L}{L_{\text{0}}}\,</math></center> | ||
<p style="text-align:right">(2)</p> | |||
< | In (2), ΔL is the change in length and L<sub>0</sub> is the object's original length. | ||
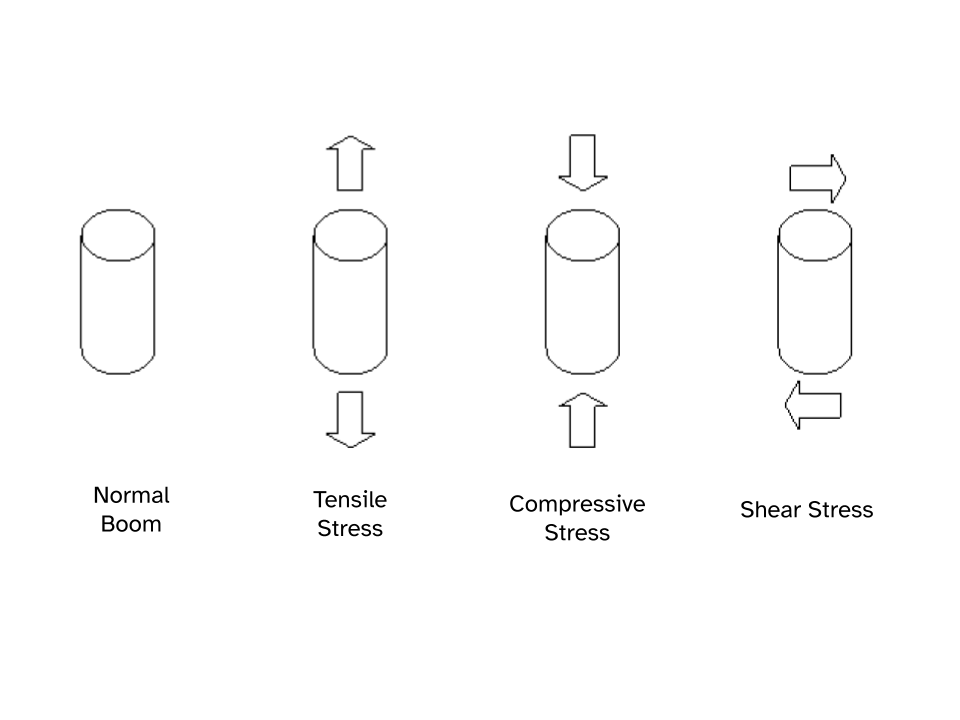
< | There are three basic types of stresses; <b>tensile</b> (pulling or stretching), <b>compressive</b> (squeezing or squashing), and <b>shear</b> (bending or cleaving). Consider a straight metal beam. If a <b>tensile stress</b> is applied to both ends, its length will increase in both directions of the force, while its cross-sectional area perpendicular to the force applied will decrease. Under <b>compressive stress</b>, the opposite will occur. If the beam is subjected to <b>shear stress</b>, it will bend towards the direction of the applied force, and both the length and cross-sectional area of the beam will become distorted. Figure 7 depicts a graphic representation of the three common forms of stress. | ||
the cross-sectional area | |||
[[Image:Lab_boom_7.gif|frame|center|Figure 7: Example of Cylindrical Material Under Three Common Modes of Stress]] | |||
Strain is proportional to stress for material dependent values of strain. If the material is known, it is possible to derive strain from measured stress, and vice-versa, up to a certain level of stress. This proportionality constant is referred to as the <b>elastic modulus</b>, or Young’s modulus. The moduli of different materials is an important factor to consider when designing or building any form of structure that will be under stresses. | |||
== Stress-Strain Curve == | |||
A <b>stress-strain</b> graphically shows the relationship between the stress and strain of a material under load. Figure 8 shows the stress-strain curve of a common metallic building material. In the <b>elastic region</b>, the material will regain its original shape once the stress is removed. The elastic region in Figure 8 is fairly linear. The slope of this linear portion of the stress-strain curve is the elastic modulus. | |||
[[Image:lab_boom_2.jpg|frame|center|Figure 8: Stress-Strain Curve of a Material Under Tension]] | |||
The <b>elastic limit</b> for a material is the maximum strain it can sustain before it becomes permanently deformed (i.e. if the stress is decreased, the object no longer returns to its original size and shape). In the <b>plastic region</b>, the material loses its elasticity and is permanently deformed. A linear approximation with the elastic modulus is no longer accurate. | |||
a material is the maximum strain it can sustain before it becomes permanently | |||
deformed (i.e. if | |||
its original size and shape). | |||
the | |||
< | The <b>ultimate tensile strength</b> is the maximum stress a material can undergo. The <b>fracture stress</b> is the point at which the material breaks. Fracture stress is lower than the ultimate tensile strength of a material because the material has reached that level of stress and has already begun to fail. The cross-sectional area is constantly decreasing until the material finally breaks. | ||
<p>The first aging factor is chemical degradation and, in particular, <b><i>corrosion</i></b>. Light and | In addition to these intrinsic materials factors, the behavior of materials as they age and are used in service must be considered in boom design. These factors are not applicable to the boom design in this lab, but they must be considered when deciding what material to use for a design. The loss of desirable properties through use, called <b>fatigue</b>, is important. Non-static loads, repeated loading and unloading, or loads that include vibrations or oscillations will eventually lead to failure in service. Special care must be taken with live loads and situations where small motions may be magnified by design features. | ||
<!--<p>The first aging factor is chemical degradation and, in particular, <b><i>corrosion</i></b>. Light and | |||
chemicals present in the | chemicals present in the | ||
| Line 150: | Line 78: | ||
rust results when iron or simple steel is exposed to water, or just even humid | rust results when iron or simple steel is exposed to water, or just even humid | ||
air. Rust is particularly damaging | air. Rust is particularly damaging | ||
because it flakes off, thinning and weakening the underlying material. Careful choice of material will minimize the effects of chemical degradation. However | because it flakes off, thinning and weakening the underlying material. Careful choice of material will minimize the effects of chemical degradation. However, | ||
cost is often limiting factor and cheap | the cost is often limiting factor and cheap countermeasures like paint and other | ||
coatings are often employed.</p> | coatings are often employed.</p> | ||
| Line 160: | Line 88: | ||
process. Care in the design process can | process. Care in the design process can | ||
help minimize the effect of erosion. | help minimize the effect of erosion. | ||
Again cost is often the limiting factor and coatings are often employed | Again the cost is often the limiting factor and coatings are often employed | ||
to protect an object.</p> | to protect an object.</p> | ||
| Line 166: | Line 94: | ||
cycling</i></b>. Materials in an object | cycling</i></b>. Materials in an object | ||
will routinely warm up and cool down while in use (especially device that | will routinely warm up and cool down while in use (especially device that | ||
generates heat internally), over the course of a normal day, or even over a | |||
year. This thermal cycling is | year. This thermal cycling is | ||
accompanied by physical expansion and contraction of the object. Different materials expand and contract by | accompanied by physical expansion and contraction of the object. Different materials expand and contract by | ||
different amounts and this can lead to internal stress and strains, and | different amounts and this can lead to internal stress and strains, and | ||
ultimately failure. Careful choice and | ultimately failure. Careful choice and | ||
matching of materials can minimize the effects of thermal cycling, but cost may | matching of materials can minimize the effects of thermal cycling, but the cost may | ||
limit the choices. Accumulations of | limit the choices. Accumulations of | ||
water, which can freeze and thaw, can be very damaging and coatings are often | water, which can freeze and thaw, can be very damaging and coatings are often | ||
| Line 188: | Line 116: | ||
treatment (annealing) and in general, material properties can be improved | treatment (annealing) and in general, material properties can be improved | ||
significantly through heat treatment and mechanical working. For example, the familiar Pyrex<sup>TM</sup> | significantly through heat treatment and mechanical working. For example, the familiar Pyrex<sup>TM</sup> | ||
glass is specially treated to avoid thermal shock.</p> | glass is specially treated to avoid thermal shock.</p>--> | ||
There are many factors to consider in any design project. When designing and constructing the boom for this competition, consider the materials being used and what might cause those materials to fail under a load. | |||
constructing | |||
=Competition Rules= | |||
The competition rules must be followed at all times during the competition. | |||
Violation of any of these rules will result in the disqualification of | Violation of any of these rules will result in the disqualification of the | ||
design. | |||
<ul> | <ul> | ||
<li> | <li>The boom is to be secured (i.e. anchored) to the white plastic anchorage provided at the front of the lab | ||
the anchorage | <li>The boom must extend at least 1.5 meters horizontally from the front edge of | ||
the anchorage</li> | |||
<li> | <li>The boom must be anchored in 2 min or less</li> | ||
<li>The boom may not touch anything but the anchorage</li> | |||
<li> | <li>The boom’s performance will be assessed by its anchor time, boom weight, boom length, and the weight it can support before deflecting 0.20 m vertically</li> | ||
</ul> | |||
< | The <b>basic weight ratio</b> (3) for the competition uses the weight supported in grams divided by the boom weight in grams. This ratio should be greater than 1. | ||
basic weight ratio for the competition | |||
<math>Weight\ Ratio = \frac{Weight\ Supported}{Boom\ Weight}\,</math> | <center><math>Weight\ Ratio = \frac{Weight\ Supported\left[\text{g}\right]}{Boom\ Weight\left[\text{g}\right]}\,</math></center> | ||
<p style="text-align:right">(3)</p> | |||
The winning design will be determined by the <b>weighted design ratio</b> (4), which uses the weight ratio, anchor time in seconds, and boom length in meters. Each component ratio should be greater than 1. | |||
<math>Design\ Ratio = \frac{Weight\ Supported}{Boom\ Weight} \times \frac{60\left[\text{s}\right]}{Anchor\ Time\left[\text{s}\right]+30\left[\text{s}\right]} \times \frac{Boom\ Length\left[\text{m}\right]}{1.5\left[\text{m}\right]}\,</math> | <center><math>Design\ Ratio = \frac{Weight\ Supported\left[\text{g}\right]}{Boom\ Weight\left[\text{g}\right]} \times \frac{60\left[\text{s}\right]}{Anchor\ Time\left[\text{s}\right]+30\left[\text{s}\right]} \times \frac{Boom\ Length\left[\text{m}\right]}{1.5\left[\text{m}\right]}\,</math></center> | ||
<p style="text-align:right">(4)</p> | |||
=Design Considerations= | |||
* Which aspects of the competition | * Which aspects of the competition ratio are most advantageous? | ||
* How can the boom be built and/or reinforced to prevent as much deflection as possible? | * How can the boom be built and/or reinforced to prevent as much deflection as possible? | ||
=Materials and Equipment= | |||
<ul> | <ul> | ||
<li> | <li>Two thick dowels (1.1 cm × 122 cm)</li> | ||
<li> | <li>Two thin dowels (0.8 cm × 122 cm)</li> | ||
<li> | <li>Six bamboo skewers (30.5 cm)</li> | ||
<li>3D | <li>3D printed dowel connectors</li> | ||
<li>Cellophane | <li>Cellophane tape</li> | ||
<li> | <li>Polyester string</li> | ||
</ul> | </ul> | ||
<font color="red"><b>'''Note: A saw is available to cut the dowels. Ask a TA for assistance, as only TAs may use the saw.'''</b></font> | |||
= Procedure = | |||
== Part 1. Boom Design and Construction == | |||
# Assess the materials and consider the design options, keeping in mind the competition specifications. Preliminary sketches must be completed during this process. | |||
# Sketch the basic design in pencil using the lab notes paper provided by a TA or on the EG1003 website. Label the design clearly and have a TA sign and date it. | |||
# Construct the boom based on the completed sketch and the available materials. A TA will provide the materials allowed for the design. If the design is modified during the construction phase, make sure to note the changes and describe the reasons for them. | |||
== Part 2. Competition == | |||
< | <p><b>Note: </b>Attaching the boom to the anchorage is a critical phase of the competition. Anchoring will be timed. Making a plan to anchor the boom quickly will improve its standing in the competition. Practice anchoring before the trial begins. The boom will be disqualified if anchoring the boom takes more than 2 min. | ||
# When the TA says "Go," attach the boom to the anchorage and shout "Done" when the boom is anchored. The TA will only stop the timer once there are no more hands are touching the boom. The TA will give the anchoring time that will be used to compute the boom's design ratio. | |||
# A TA will measure the boom length and record the length in the competition spreadsheet for the section. | |||
competition | # A TA will attach a basket to the end of the boom and add weights until the boom deflects (bends) 0.20 m vertically. The load supported will be weighed on the lab scale and recorded in the competition spreadsheet for the section. | ||
# A TA will weigh the boom and record the weight in the competition spreadsheet for the section. | |||
# The design ratio for the in-person boom design will be used to decide the winner of the competition. | |||
< | <p>A TA will prepare an Excel file with the section's results. It can be accessed in the [http://eg.poly.edu/documents.php Lab Documents] section of the EG1003 website. This chart must be included in the PowerPoint presentation and in the Data/Observations section of the lab report. The lab work is now complete. Please clean up the workstation. Return all unused materials to a TA. Refer to the Assignment section for the instructions to prepare the lab report. | ||
=Assignment= | |||
== Individual Lab Report == | |||
{{Ambox | |||
</ | | type = notice | ||
| text = <h4>Extra Credit Opportunity</h4>Students who perform well on this report have the opportunity to replace a lower score on an earlier lab report with their score on this report.}} | |||
{{Labs:Lab Report}} | |||
* What factors were considered in designing the boom? Discuss the background information that was used | |||
* Describe the competition rules in the Introduction. What impact did the rules and ratios have on any design decisions? | |||
* Describe the function of each component used in the design | |||
* Describe the advantages and disadvantages of the boom design | |||
* Discuss potential design improvements. How can the design be optimized (i.e. improve the design ratio) from this lab experience? | |||
* Which elements of the boom were stressed by the load? Describe the load’s direction and if the load contributed s to the failure? | |||
* Include the Excel spreadsheet with all the boom designs in the class. Discuss other designs in the class | |||
* Contribution Statement | |||
{{Labs:Lab Notes}} | |||
< | <h3>Team PowerPoint Presentation</h3> | ||
PowerPoint | |||
{{Labs:Team Presentation}} | |||
<ul> | <ul> | ||
<li> | <li>How can the boom design be improved?</li> | ||
<li>Other than the examples given in this lab, what are other boom examples in the real world?</li> | |||
<li>Which elements of the boom (e.g., wooden dowels, 3D printed dowel connectors, Kevlar string, etc.,) were stressed by the load, in what directions, and could potentially lead to the failure? | |||
<li> | |||
<li>Which elements of the boom (e.g., wooden dowels, 3D printed dowel connectors, Kevlar string, etc.,) were stressed by the load, in what directions, and | |||
</ul> | </ul> | ||
= References = | |||
< | <i>How Stuff Works</i> website. 2003. SHW Media Network. Retrieved July 28, 2003. | ||
http://science.howstuffworks.com/tower-crane3.htm | |||
Jennings, James. 2015. “Up, UP in a Crane: What Life is Like as a Tower Crane Operator.” Philadelphia. Accessed 14 January 2020 from www.phillymag.com | |||
Serway, R., Beichner, R., <i>Physics for Scientists and Engineers with Modern Physics, 5</i><i><sup>th</sup></i> Edition. Fort Worth, TX: Saunders College Publishing, 2000 | |||
{{Laboratory Experiments}} | |||
Revision as of 17:33, 23 March 2022
Objective
The experimental objective of this lab is to design and assemble a boom. This is a competition lab, and the booms will be judged by a design ratio that uses boom weight, boom length, weight held, and anchor time. The highest design ratio wins the competition.
Overview
A boom is used to lift and move heavy objects, often objects that are much heavier than the boom itself. Distributing the load being lifted over the length of the boom is the main problem in boom design. The design must consider the maximum load the boom will be required to lift, how high the load will be lifted, and whether the boom will be moved or remain stationary while loaded.
Examples of Booms
Certain types of bridges use booms. A cantilever bridge uses two booms extending from a common base. One type of cantilever bridge is a cable-stayed bridge (Figure 1).
The Ed Koch Queensboro Bridge is a double cantilever bridge (Figure 2). It has two bases with two booms extending from each base and the cantilevers placed end to end.
The Grand Bridge over Newtown Creek is a swing bridge, also known as a rotating bridge (Figure 3). This bridge has two booms mounted on a base that rotates.
Figure 4 shows a bascule bridge, more commonly known as a drawbridge, where it is clear that the bridge uses a big, very flat boom.
Not all bridges are booms. Suspension bridges use a deck that is supported by steel cables, not booms. Examples of suspension bridges are the Brooklyn Bridge, Manhattan Bridge, Verrazano-Narrows Bridge, and the George Washington Bridge.
Cranes are the most common example of booms. The crane pictured in Figure 5 is a tower crane. These cranes are a fixture on construction sites around the world. A tower crane can lift a 40,000 lb load. It is attached to the ground by anchor bolts driven through a 400,000 lb concrete pad poured a few weeks before the crane is erected (Howstuffworks.com, 2003).
Stress and Strain
The design of a boom must consider the properties of the materials used to build the boom. The mechanical properties and deformation of solids are explained by stress and strain. When an external force is applied to a material, it changes shape (e.g. changes length and cross-section perpendicular to the length). Understanding how deformation will affect materials is a critical consideration in boom design.
According to Serway and Beichner in “Physics for Scientists and Engineers,” stress is the external force acting on an object per unit cross sectional area. Strain is the measure of deformation resulting from an applied stress (Figure 6).
The expression (1) for tensile stress shows the relationship between an applied force and the cross-sectional area.
(1)
In (1), σ is the stress, F is the applied force, and A is the cross-sectional area of the object perpendicular to the force. The resulting strain (2) is calculated by dividing the change in length of the object by the original length.
(2)
In (2), ΔL is the change in length and L0 is the object's original length.
There are three basic types of stresses; tensile (pulling or stretching), compressive (squeezing or squashing), and shear (bending or cleaving). Consider a straight metal beam. If a tensile stress is applied to both ends, its length will increase in both directions of the force, while its cross-sectional area perpendicular to the force applied will decrease. Under compressive stress, the opposite will occur. If the beam is subjected to shear stress, it will bend towards the direction of the applied force, and both the length and cross-sectional area of the beam will become distorted. Figure 7 depicts a graphic representation of the three common forms of stress.
Strain is proportional to stress for material dependent values of strain. If the material is known, it is possible to derive strain from measured stress, and vice-versa, up to a certain level of stress. This proportionality constant is referred to as the elastic modulus, or Young’s modulus. The moduli of different materials is an important factor to consider when designing or building any form of structure that will be under stresses.
Stress-Strain Curve
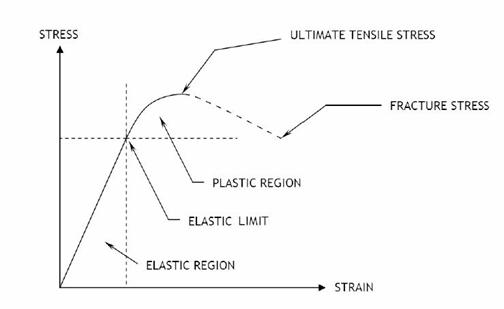
A stress-strain graphically shows the relationship between the stress and strain of a material under load. Figure 8 shows the stress-strain curve of a common metallic building material. In the elastic region, the material will regain its original shape once the stress is removed. The elastic region in Figure 8 is fairly linear. The slope of this linear portion of the stress-strain curve is the elastic modulus.
The elastic limit for a material is the maximum strain it can sustain before it becomes permanently deformed (i.e. if the stress is decreased, the object no longer returns to its original size and shape). In the plastic region, the material loses its elasticity and is permanently deformed. A linear approximation with the elastic modulus is no longer accurate.
The ultimate tensile strength is the maximum stress a material can undergo. The fracture stress is the point at which the material breaks. Fracture stress is lower than the ultimate tensile strength of a material because the material has reached that level of stress and has already begun to fail. The cross-sectional area is constantly decreasing until the material finally breaks.
In addition to these intrinsic materials factors, the behavior of materials as they age and are used in service must be considered in boom design. These factors are not applicable to the boom design in this lab, but they must be considered when deciding what material to use for a design. The loss of desirable properties through use, called fatigue, is important. Non-static loads, repeated loading and unloading, or loads that include vibrations or oscillations will eventually lead to failure in service. Special care must be taken with live loads and situations where small motions may be magnified by design features.
There are many factors to consider in any design project. When designing and constructing the boom for this competition, consider the materials being used and what might cause those materials to fail under a load.
Competition Rules
The competition rules must be followed at all times during the competition. Violation of any of these rules will result in the disqualification of the design.
- The boom is to be secured (i.e. anchored) to the white plastic anchorage provided at the front of the lab
- The boom must extend at least 1.5 meters horizontally from the front edge of the anchorage
- The boom must be anchored in 2 min or less
- The boom may not touch anything but the anchorage
- The boom’s performance will be assessed by its anchor time, boom weight, boom length, and the weight it can support before deflecting 0.20 m vertically
The basic weight ratio (3) for the competition uses the weight supported in grams divided by the boom weight in grams. This ratio should be greater than 1.
(3)
The winning design will be determined by the weighted design ratio (4), which uses the weight ratio, anchor time in seconds, and boom length in meters. Each component ratio should be greater than 1.
(4)
Design Considerations
- Which aspects of the competition ratio are most advantageous?
- How can the boom be built and/or reinforced to prevent as much deflection as possible?
Materials and Equipment
- Two thick dowels (1.1 cm × 122 cm)
- Two thin dowels (0.8 cm × 122 cm)
- Six bamboo skewers (30.5 cm)
- 3D printed dowel connectors
- Cellophane tape
- Polyester string
Note: A saw is available to cut the dowels. Ask a TA for assistance, as only TAs may use the saw.
Procedure
Part 1. Boom Design and Construction
- Assess the materials and consider the design options, keeping in mind the competition specifications. Preliminary sketches must be completed during this process.
- Sketch the basic design in pencil using the lab notes paper provided by a TA or on the EG1003 website. Label the design clearly and have a TA sign and date it.
- Construct the boom based on the completed sketch and the available materials. A TA will provide the materials allowed for the design. If the design is modified during the construction phase, make sure to note the changes and describe the reasons for them.
Part 2. Competition
Note: Attaching the boom to the anchorage is a critical phase of the competition. Anchoring will be timed. Making a plan to anchor the boom quickly will improve its standing in the competition. Practice anchoring before the trial begins. The boom will be disqualified if anchoring the boom takes more than 2 min.
- When the TA says "Go," attach the boom to the anchorage and shout "Done" when the boom is anchored. The TA will only stop the timer once there are no more hands are touching the boom. The TA will give the anchoring time that will be used to compute the boom's design ratio.
- A TA will measure the boom length and record the length in the competition spreadsheet for the section.
- A TA will attach a basket to the end of the boom and add weights until the boom deflects (bends) 0.20 m vertically. The load supported will be weighed on the lab scale and recorded in the competition spreadsheet for the section.
- A TA will weigh the boom and record the weight in the competition spreadsheet for the section.
- The design ratio for the in-person boom design will be used to decide the winner of the competition.
A TA will prepare an Excel file with the section's results. It can be accessed in the Lab Documents section of the EG1003 website. This chart must be included in the PowerPoint presentation and in the Data/Observations section of the lab report. The lab work is now complete. Please clean up the workstation. Return all unused materials to a TA. Refer to the Assignment section for the instructions to prepare the lab report.
Assignment
Individual Lab Report
Extra Credit OpportunityStudents who perform well on this report have the opportunity to replace a lower score on an earlier lab report with their score on this report. |
Follow the lab report guidelines laid out in the EG1004 Writing Style Guide in the Technical Writing section of the manual. Use the outline below to write this report.
- What factors were considered in designing the boom? Discuss the background information that was used
- Describe the competition rules in the Introduction. What impact did the rules and ratios have on any design decisions?
- Describe the function of each component used in the design
- Describe the advantages and disadvantages of the boom design
- Discuss potential design improvements. How can the design be optimized (i.e. improve the design ratio) from this lab experience?
- Which elements of the boom were stressed by the load? Describe the load’s direction and if the load contributed s to the failure?
- Include the Excel spreadsheet with all the boom designs in the class. Discuss other designs in the class
- Contribution Statement
Remember: Lab notes must be taken. Experimental details are easily forgotten unless written down. EG1004 Lab Notes paper can be downloaded and printed from the EG1004 Website. Use the lab notes to write the Procedure section of the lab report. At the end of each lab, a TA will scan the lab notes and upload them to the Lab Documents section of the EG1004 Website. One point of extra credit is awarded if the lab notes are attached at the end of the lab report. Keeping careful notes is an essential component of all scientific practice.
Team PowerPoint Presentation
Follow the presentation guidelines laid out in the EG1004 Lab Presentation Format in the Technical Presentations section of the manual. When preparing the presentation, consider the following points.
- How can the boom design be improved?
- Other than the examples given in this lab, what are other boom examples in the real world?
- Which elements of the boom (e.g., wooden dowels, 3D printed dowel connectors, Kevlar string, etc.,) were stressed by the load, in what directions, and could potentially lead to the failure?
References
How Stuff Works website. 2003. SHW Media Network. Retrieved July 28, 2003. http://science.howstuffworks.com/tower-crane3.htm
Jennings, James. 2015. “Up, UP in a Crane: What Life is Like as a Tower Crane Operator.” Philadelphia. Accessed 14 January 2020 from www.phillymag.com
Serway, R., Beichner, R., Physics for Scientists and Engineers with Modern Physics, 5th Edition. Fort Worth, TX: Saunders College Publishing, 2000
| ||||||||





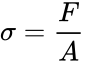
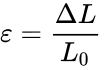
![{\displaystyle Weight\ Ratio={\frac {Weight\ Supported\left[{\text{g}}\right]}{Boom\ Weight\left[{\text{g}}\right]}}\,}](https://wikimedia.org/api/rest_v1/media/math/render/png/472aaf7be956720961e3a74beaacadc2249fe44d)
![{\displaystyle Design\ Ratio={\frac {Weight\ Supported\left[{\text{g}}\right]}{Boom\ Weight\left[{\text{g}}\right]}}\times {\frac {60\left[{\text{s}}\right]}{Anchor\ Time\left[{\text{s}}\right]+30\left[{\text{s}}\right]}}\times {\frac {Boom\ Length\left[{\text{m}}\right]}{1.5\left[{\text{m}}\right]}}\,}](https://wikimedia.org/api/rest_v1/media/math/render/png/5793bb34f29b6d3a7f2d185f01db3b198ed94819)